题目内容
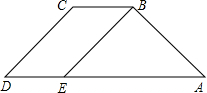 如图,若AD∥BC,∠A=∠D.
如图,若AD∥BC,∠A=∠D.(1)猜想∠C与∠ABC的数量关系,并说明理由;
(2)若CD∥BE,∠D=50°,求∠EBC的度数.
考点:平行线的性质
专题:
分析:(1)先根据平行线的性质得出∠D+∠C=180°,∠A+∠ABC=180°,再根据∠A=∠D即可得出结论;
(2)根据CD∥BE可得出∠D=∠AEB,再由AD∥BC即可得出结论.
(2)根据CD∥BE可得出∠D=∠AEB,再由AD∥BC即可得出结论.
解答:解:(1)∵AD∥BC,
∴∠D+∠C=180°,∠A+∠ABC=180°,
∵∠A=∠D,
∴∠C=∠ABC;
(2)∵CD∥BE,
∴∠D=∠AEB.
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠D=∠EBC=50°.
∴∠D+∠C=180°,∠A+∠ABC=180°,
∵∠A=∠D,
∴∠C=∠ABC;
(2)∵CD∥BE,
∴∠D=∠AEB.
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠D=∠EBC=50°.
点评:本题考查的是平行线的性质,用到的知识点为;两直线平行,同旁内角互补.

练习册系列答案
相关题目
若m与n为正整数,xm+yn+2m+n的次数是( )
| A、m | B、n |
| C、m+n | D、m,n中较大的数 |
下列方程中是一元二次方程的是( )
| A、(x-1)(2x+3)=2x(x+1) | ||
| B、ax2+bx+c=0 | ||
C、4x-
| ||
| D、(2a+3)(4a-1)=0 |
按下列长度,A、B、C三点一定不在同一条直线上的是( )
| A、AB=5.6cm,BC=4.5cm,AC=10.1cm |
| B、AB=2.7cm,BC=3.9cm,AC=5.6cm |
| C、AB=5cm,BC=6cm,AC=11cm |
| D、AB=15cm,BC=5cm,AC=10cm |
下列各点落在x轴上的是( )
| A、(1,0) |
| B、(0,1) |
| C、(1,1) |
| D、(-1,-1) |
 反比例函数y=
反比例函数y=


