题目内容
若代数式a2+a=1,求a4+2a3-3a2-4a+3的值.
考点:因式分解的应用
专题:
分析:根据所给代数式的结构特点,运用因式分解法逐步将次,即可解决问题.
解答:解:∵a2+a=1,
∴a4+2a3-3a2-4a+3
=a2(a2+a)+a3-3a2-4a+3
=a2+a3-3a2-4a+3
=a3-2a2-4a+3
=a(1-a)-2a2-4a+3
=a-a2-2a2-4a+3
=-3a2-3a+3
=-3(a2+a-1)
=0.
∴a4+2a3-3a2-4a+3
=a2(a2+a)+a3-3a2-4a+3
=a2+a3-3a2-4a+3
=a3-2a2-4a+3
=a(1-a)-2a2-4a+3
=a-a2-2a2-4a+3
=-3a2-3a+3
=-3(a2+a-1)
=0.
点评:该题主要考查了因式分解及其应用问题;解题的关键是根据所给代数式的结构特点,灵活运用因式分解法来变形、化简、计算、求值.

练习册系列答案
相关题目
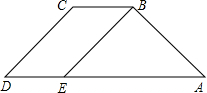 如图,若AD∥BC,∠A=∠D.
如图,若AD∥BC,∠A=∠D.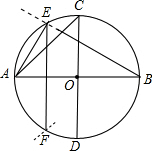 如图,在⊙O中,如果作两条互相垂直的直径AB、CD,那么弦AC是⊙O的内接正方形的一边;如果以点A为圆心,以OA为半径画弧,与⊙O相交于点E,F,那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边,为什么?
如图,在⊙O中,如果作两条互相垂直的直径AB、CD,那么弦AC是⊙O的内接正方形的一边;如果以点A为圆心,以OA为半径画弧,与⊙O相交于点E,F,那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边,为什么?