题目内容
15.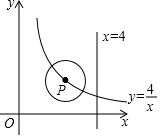 如图,P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线x=4相切时,点P的坐标为(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).
如图,P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线x=4相切时,点P的坐标为(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).
分析 利用切线的性质以及反比例函数的性质即可得出,P点的坐标应该有两个求出即可.
解答 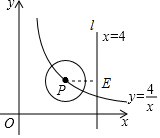 解:过点P作AE⊥l于点E,
解:过点P作AE⊥l于点E,
当⊙P在直线的左侧时,P点横坐标为4-1=3,
∵P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,
∴P(3,$\frac{4}{3}$).
当⊙P在直线的右侧时,P点横坐标为4+1=5,
∴P(5,$\frac{4}{5}$).
综上所述,P点坐标为:(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).
故答案为:(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).
点评 本题考查的是反比例函数图象上点的坐标特点,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.江油这个春节旅游窗口大放异彩,取得开门红,据统计春节期间旅游综合收入40619.94万元,请你把40619.94万元用科学记数法表示为( )
| A. | 4.061994×105万元 | B. | 4.061994×106万元 | ||
| C. | 4.061994×104万元 | D. | 40.61994×103万元 |
20.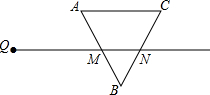 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )
 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )| A. | t=2 | B. | 3≤t≤7 | C. | t=8 | D. | t=2或3≤t≤7或t=8 |
7.计算$\sqrt{27}$-$\sqrt{8}$•$\sqrt{\frac{2}{3}}$的结果是( )
| A. | $\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{3}$ | C. | $\frac{5}{3}\sqrt{3}$ | D. | $2\sqrt{3}$ |
 某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,$\sqrt{3}$≈1.73)
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,$\sqrt{3}$≈1.73)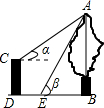 如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)
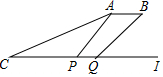
如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号) 如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=3-$\sqrt{5}$.
如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=3-$\sqrt{5}$.