题目内容
18．将正偶数按表1排成5列：| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … | … |
| A． | 第252行，第4列 | B． | 第252行，第3列 | C． | 第251行，第4列 | D． | 第251行，第2列 |
分析 根据题意得到每一行是4个偶数，奇数行从第2列往后排，偶数行从第4列往前排，然后用2010除以2得到2010是第1005个偶数，再用1005÷4得251余1，于是可判断2010的位置．
解答 解：∵2010÷2=1005
∴2010是第1005个偶数，
而1005÷4=251…1，
∴第1005个偶数在第252行，
∵偶数行的数从第4列开始向前面排，
∴第1005个偶数在第4列，
∴2010应在第252行第4列，
故选：A．
点评 本题考查了关于数字的变化规律：先要观察各行各列的数字的特点，得出数字排列的规律，然后确定所给数字的位置．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在△ABC中，D、E分别是AB、AC的中点，若BC=12，则DE=6．
13．邮递员从山坡下的邮局出发，骑自行车到达山坡顶后，停下一段时间分发邮件，之后沿原路返回邮局，设邮递员从邮局出发后所用的时间为x（分钟），邮递员与邮局的距离为y（米），则y与x的函数图象大致是（ ）
| A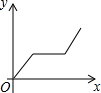． |  | B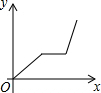． |  | C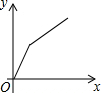． |  | D． |  |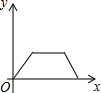
7．下列说法正确的是（ ）
| A． | 当a=-6时，-a的相反数是+6 | |
| B． | 如果a，b都是有理数且|a|＞|b|，那么a＞b | |
| C． | 如果|a-2|+（1+b）2=0，那么ba=1 | |
| D． | 如果a、b互为相反数，c、d互为倒数，那么$\frac{a+b}{2}$-cd=1 |
8．求一个正数的立方根，有些数可以直接求得，如$\root{3}{8}$=2，有些数则不能直接求得，如$\root{3}{9}$，但可以利用计算器求得，还可以通过一组数的内在联系，运用规律求得，请同学观察下表：
已知$\root{3}{2.16}$≈1.293，$\root{3}{21.6}$≈2.785，$\root{3}{216}$≈6，运用你发现的规律求$\root{3}{21600000}$=278.5．
| n | 0.008 | 8 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 0.2 | 2 | 20 | 200 | … |