题目内容
10.已知两条线段的长分别为$\sqrt{6}$和$\sqrt{10}$,当第三条线段为4或2时,这三条线段能围成一个直角三角形?若等腰直角三角形的斜边长为2,它的一条直角边的长是$\sqrt{2}$.分析 由于直角三角形的斜边不能确定,故应分$\sqrt{10}$为直角边和斜边两种情况进行讨论.
利用勾股定理,设直角边为a,则2a2=4求解即可.
解答 解:当$\sqrt{10}$为直角边时,设斜边为x,则($\sqrt{10}$)2+($\sqrt{6}$)2=x2,解得x=±4(负值舍去);
当$\sqrt{10}$为斜边时,设另一直角边为x,则($\sqrt{10}$)2=($\sqrt{6}$)2+x2,解得x=±2(负值舍去).
∵三角形为等腰直角三角形,
∴设两直角边为a,则
a2+a2=22,
解得a═±$\sqrt{2}$(负值舍去).
故答案为:4或2;$\sqrt{2}$.
点评 本题考查的是勾股定理的逆定理,在解答此题时要注意分类讨论.第(2)问需注意根据等腰直角三角形的特点,利用勾股定理进行解答,还要注意,三角形的边长是正值.

练习册系列答案
相关题目
18.下列方程中是一元二次方程的是( )
| A. | x2+1=0 | B. | y2+x=1 | C. | 2x+1=0 | D. | x+$\frac{1}{x}$=1 |
15.若132x=64,则13-x=( )
| A. | -$\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | $\frac{1}{80}$ | D. | $\frac{1}{512}$ |
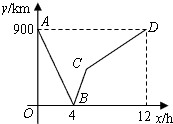 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y,图中的折线表示y与x之间的函数关系.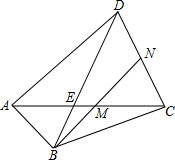 如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点.
如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点. 已知:如图,直线l是线段AB的垂直平分线,C、D是l上任意两点(除AB的中点外).求证:∠CAD=∠CBD.
已知:如图,直线l是线段AB的垂直平分线,C、D是l上任意两点(除AB的中点外).求证:∠CAD=∠CBD.