题目内容
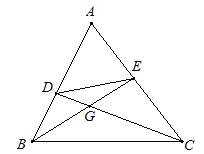
【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
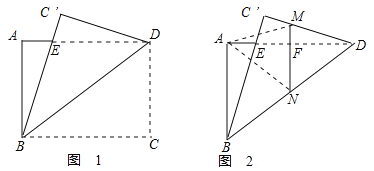
【答案】![]()
【解析】
由折叠的性质可知△DFM为直角三角形,且DF=![]() AD=2,可证△ABE≌△
AD=2,可证△ABE≌△![]() DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
解:如图,由已知可得MN垂直平分AD,DF=![]() AD=2,FN=
AD=2,FN=![]() AB=
AB=![]() ,
,
∵AB=CD=![]() D,∠A=∠
D,∠A=∠![]() =90°,∠AEB=∠
=90°,∠AEB=∠![]() ED,
ED,
∴△ABE≌△![]() DE,∴BE=ED, ∠ABE=∠
DE,∴BE=ED, ∠ABE=∠![]() DE
DE
设AE=x,则BE=ED=4-x,
在Rt△ABE中,由勾股定理得
AB2+AE2=BE2,即32+x2=(4-x)2,
解得x=![]() ,∴AE=
,∴AE=![]()
∵∠ABE=∠![]() DE, ∠BAE=∠
DE, ∠BAE=∠![]() =90°,
=90°,
∴△ABE∽△FDM,
∴![]() =
=![]() ,即
,即  ,
,
解得MF=![]() .
.
∴MN=NF+FM=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
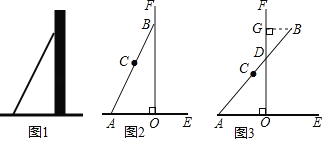
小学生10分钟应用题系列答案【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
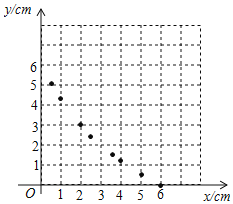
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.