Question

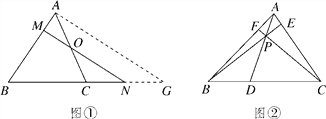
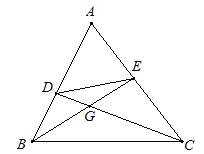
【题目】已知：如图，在△ABC中，点D、E分别在边AB、AC上，且∠ABE =∠ACD，BE、CD交于点G．

（1）求证：△AED∽△ABC；

（2）如果BE平分∠ABC，求证：DE=CE．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

试题（1）先证△ABE∽△ACD，得出，再利用∠A是公共角，即可求证；（2）在BC上截取BF=BD，连接EF，先证△BDE≌△BFE，得出DE=FE，∠BDE=∠BFE，再证EF=EC即可.

解：（1）∵∠ABE =∠ACD，且∠A是公共角，

∴△ABE∽△ACD．

∴，即，

又∵∠A是公共角，

∴△AED∽△ABC．

（2）在BC上截取BF=BD，连接EF，

在△BDE与△BFE中，BD=BF,∠DBE=∠FBE，BE=BE，

∴△BDE≌△BFE，

∴DE=FE，∠BDE=∠BFE，∴∠ADE=∠EFC，

∵△AED∽△ABC，∴∠ADE=∠ACB，

∴∠EFC=∠ACB，

∴EF=EC，

∴DE=CE．