题目内容
【题目】已知二次函数y=
（1）将其配方成顶点式，并写出它的图象的开口方向、顶点坐标、对称轴．
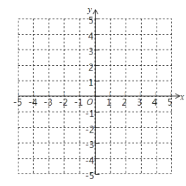
（2）在如图所示的直角坐标系中画出函数图象，并指出当y＜0时x的取值范围．
【答案】（1）抛物线的图象的开口向上、顶点坐标为（1，﹣
）、对称轴为直线x=1；（2）当﹣1＜x＜3时，y＜0，图像见解析
【解析】
（1）利用配方法得到
，然后根据二次函数的性质求解；
（2）先求出抛物线与
轴的交点坐标，然后利用描点法画二次函数图象，再写出函数图象在轴下方所对应的自变量的范围即可；
（3）利用函数图象，得到
时函数值最小，
时函数值最大．
解：（1）
，
所以抛物线的图象的开口向上、顶点坐标为
、对称轴为直线；
（2）当
时，
，解得
，
，抛物线与轴的交点坐标为
，
，抛物线如图，
当
时，
；
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
