题目内容
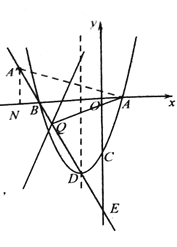
【题目】己知抛物线![]() 与x轴交于A,B两点(点d在点B的右侧),与y轴交于点
与x轴交于A,B两点(点d在点B的右侧),与y轴交于点![]() ,顶点为D.
,顶点为D.
(I)求该抛物线的解析式及顶点D的坐标:
(Ⅱ)Q为线段BD上一点,点A关于∠AQB的平分线的对称点为A',
①判断点A'与直线BQ的位置关系:点![]() (填写“在”或“不在”)直线BQ上:
(填写“在”或“不在”)直线BQ上:
②若![]() ,求点2的坐标:
,求点2的坐标:
(Ⅲ)若此抛物线的对称轴上的点P满足![]() ,求点P的坐标。
,求点P的坐标。
【答案】(I)![]() ,顶点D的坐标为
,顶点D的坐标为![]() ;(II)①在; ②点Q的坐标为
;(II)①在; ②点Q的坐标为![]() ;(Ⅲ)点P的坐标为
;(Ⅲ)点P的坐标为![]() 或
或![]()
【解析】
(1)将C点代入函数解析式,可求出解析式,并进行配方,即可得到定点坐标;
(2)①由对称的角度特点及角平线即可判断A'与直线BQ的位置关系;
②先求出抛物线与x轴胡交点,在求出BD的解析式,从而得到E点坐标,根据![]() ,A’点坐标,从而
,A’点坐标,从而![]() ,建立方程即可求解.
,建立方程即可求解.
(3)作△ABC的外接圆![]() ,由题意可知P在圆I与二次函数的对称轴上,再根据内心的特点得
,由题意可知P在圆I与二次函数的对称轴上,再根据内心的特点得![]() ,从而建立方程得到I胡坐标,根据
,从而建立方程得到I胡坐标,根据![]() 即可求解.
即可求解.
解:(I)把点C的坐标代入地物线解析式,得![]() ,
,
解得![]()
故该抛物线的解析式为![]()
![]()
∴顶点D的坐标为![]()
(II)①在
②∵点A关于![]() 的平分线的对称点为
的平分线的对称点为![]()
![]()
![]() 三点在一条直线上,且
三点在一条直线上,且![]()
![]()
当![]() 时,
时,![]()
解得![]()
![]()
设直线BD的解析式为![]() ,
,
由![]() ,得直线BD的解析式为
,得直线BD的解析式为![]()
直线BD与y轴交点为![]()
作![]() 轴于点N
轴于点N
∵点Q在线段BD上,![]() 三点在一条直线上,
三点在一条直线上,
![]()
![]()
![]()
![]()
![]()
∴点![]() 的坐标为
的坐标为![]()
∵点Q在线段BD上,
设点Q的坐标为![]() ,其中
,其中![]()
![]()
![]()
解得![]()
![]() 在
在![]() 内
内
∴点Q的坐标为![]()
(Ⅲ)作△ABC的外接圆![]() ,设
,设![]() 与抛物线的对轴位于x轴下方的部分的交点为点P,点P关于x轴的对称点为点
与抛物线的对轴位于x轴下方的部分的交点为点P,点P关于x轴的对称点为点![]()
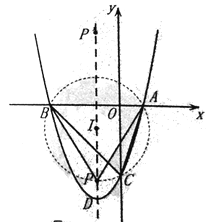
可知圆心I必在AB边的垂直平分线即抛物线的对称辅直线![]() 上
上
![]() 都是
都是![]() 所对的圆周角,
所对的圆周角,
![]()
设圆心![]()
由![]() ,得
,得![]()
![]()
点P的坐标为![]()
由对称性得点![]() 的坐标为
的坐标为![]()
符合题意的点P的坐标为![]() 或
或![]()

练习册系列答案
相关题目