��Ŀ����
9�� ��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��AOBΪ����A��B������ֱ�ΪA��0��4����B��-3��0������Ҫ�����������⣮
��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��AOBΪ����A��B������ֱ�ΪA��0��4����B��-3��0������Ҫ�����������⣮��1����ͼ�У��Ƚ���AOB����ƽ��6����λ��������ƽ��3����λ������ƽ�ƺ�ġ�A1O1B1�������е�A��O��B�Ķ�Ӧ��ΪA1��O1��B1��
��2����ͼ�У�����A1O1B1�Ƶ�O1˳ʱ����ת90�㣬������ת���Rt��A2O1B2�������е�A1��B1�Ķ�Ӧ��ΪA2��B2��
��3��ֱ��д����A2��B2�����꣮
���� ��1������ƽ�Ƶ�����д��A��O��B�Ķ�Ӧ��A1��O1��B1�����꣬Ȼ����㼴�ɵõ���A1O1B1��
��2�����������ص����ת�����ʣ�������A1��B1�Ķ�Ӧ��A2��B2���ɣ�
��3����������ͼ�Σ�д����A2��B2�����꣮
��� �⣺��1����ͼ����A1O1B1Ϊ����
��2����ͼ��Rt��A2O1B2Ϊ������
��3����A2��B2������ֱ�Ϊ��7��6������3��9����
���� ���⿼������ͼ-��ת�任��������ת�����ʿ�֪����Ӧ�Ƕ���ȶ�������ת�ǣ���Ӧ�߶�Ҳ��ȣ��ɴ˿���ͨ������ȵĽǣ��ڽǵı��Ͻ�ȡ��ȵ��߶εķ������ҵ���Ӧ�㣬˳�����ӵó���ת���ͼ�Σ�Ҳ��������ԳƱ任��

��ϰ��ϵ�д�
�����Ŀ
19��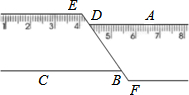 ��ͼ��һ�ѳ�����ֱ����ֱ�߶Ͽ�����λ������ͬѧ���ֵ�E��D��B��F��ͬһ��ֱ���ϣ�����ADE=115�㣬���DBC�Ķ���Ϊ��������
��ͼ��һ�ѳ�����ֱ����ֱ�߶Ͽ�����λ������ͬѧ���ֵ�E��D��B��F��ͬһ��ֱ���ϣ�����ADE=115�㣬���DBC�Ķ���Ϊ��������
 ��ͼ��һ�ѳ�����ֱ����ֱ�߶Ͽ�����λ������ͬѧ���ֵ�E��D��B��F��ͬһ��ֱ���ϣ�����ADE=115�㣬���DBC�Ķ���Ϊ��������
��ͼ��һ�ѳ�����ֱ����ֱ�߶Ͽ�����λ������ͬѧ���ֵ�E��D��B��F��ͬһ��ֱ���ϣ�����ADE=115�㣬���DBC�Ķ���Ϊ��������| A�� | 55�� | B�� | 65�� | C�� | 75�� | D�� | 125�� |
17�����к����У��Ƿ������������ǣ�������
| A�� | y=$\frac{x}{2}$ | B�� | y=-$\frac{\sqrt{3}}{3x}$ | C�� | y=$\frac{2}{{x}^{2}}$ | D�� | y=1-$\frac{1}{x}$ |
14��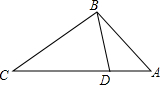 ��ͼ����D�ڡ�ABC�ı�AC�ϣ�Ҫ�жϡ�ADC���ABC���ƣ�����һ������������ȷ���ǣ�������
��ͼ����D�ڡ�ABC�ı�AC�ϣ�Ҫ�жϡ�ADC���ABC���ƣ�����һ������������ȷ���ǣ�������
 ��ͼ����D�ڡ�ABC�ı�AC�ϣ�Ҫ�жϡ�ADC���ABC���ƣ�����һ������������ȷ���ǣ�������
��ͼ����D�ڡ�ABC�ı�AC�ϣ�Ҫ�жϡ�ADC���ABC���ƣ�����һ������������ȷ���ǣ�������| A�� | ��ABD=��C | B�� | ��ADB=��ABC | C�� | CB2=CD•CA | D�� | AB2=AD•AC |
18��Ҫ˵�����⡰��a��b����|a|��|b|���Ǽ����⣬�ܾٵ�һ�������ǣ�������
| A�� | a=3��b=2 | B�� | a=4��b=-1 | C�� | a=1��b=0 | D�� | a=1��b=-2 |
19����֪x=1��y=2�Ƿ���ax+y=5��һ��⣬��a��ֵ�ǣ�������
| A�� | -3 | B�� | -2 | C�� | 3 | D�� | 7 |
 ��ͼ����·AB���������Ƿֱ���C��D����Ϊ�����ƶ����÷�չ�����Ƕ�Ҫ���ھ��Լ����������A��B��������վ����Э�����������������C��D������ȵ�E������һ����վ�����CA=10km��DB=30km��AB=50km��
��ͼ����·AB���������Ƿֱ���C��D����Ϊ�����ƶ����÷�չ�����Ƕ�Ҫ���ھ��Լ����������A��B��������վ����Э�����������������C��D������ȵ�E������һ����վ�����CA=10km��DB=30km��AB=50km��