��Ŀ����
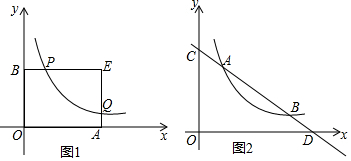
16�� ��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���OΪ����ԭ�㣬����A��C������ֱ�Ϊ��0��-$\sqrt{2}$������2$\sqrt{2}$��0����������OABC�Ƶ�O˳ʱ����ת45��õ�����OA��B��C�䣬��A��B����y�ύ�ڵ�D����������ԭ���������y=ax2+bxͬʱ������A�䡢C�䣮
��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���OΪ����ԭ�㣬����A��C������ֱ�Ϊ��0��-$\sqrt{2}$������2$\sqrt{2}$��0����������OABC�Ƶ�O˳ʱ����ת45��õ�����OA��B��C�䣬��A��B����y�ύ�ڵ�D����������ԭ���������y=ax2+bxͬʱ������A�䡢C�䣮��1��������������Ӧ�ĺ�������ʽ��
��2��д����B������ꣻ
��3����P�DZ�OC����һ�㣬����P��PQ��OC�䣬��������λ��y���Ҳಿ���ڵ�Q������OQ��DQ�����ODQ�����ΪS����ֱ��PQ������OA��B��C��������Ϊ1��3��������ʱ����S��ֵ��
��4�����־���OA��B��C�䲻����������OABC������OC'������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���ƽ��ʱ��Ϊt�루t��0����������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ����ʱ��ֱ��д��t��ȡֵ��Χ��
���� ��1�����A��C�������꣬��A��C�����������y=ax2+bx�ⷽ���鼴�ɣ�
��2����ͼ1�У�����A��C�䣬OB�佻�ڵ�E�������E���꣬�����е����깫ʽ���ɽ�����⣮
��3�����������ٵ�OP��PC��=1��3ʱ��P��$\frac{1}{2}$��-$\frac{1}{2}$�������ֱ��PQ�Ľ���ʽ�����÷����������Q���꼴�ɣ��ڵ�OP�䣺P��C��=3��1ʱ��P�䣨$\frac{3}{2}$��-$\frac{3}{2}$�����������ƣ�
��4����ͼ3�У�����A��A��B����ʱ���ص��������ı���AMON������Գ�ͼ�Σ���OM=AMʱ����ʱ$\sqrt{2}$t=$\sqrt{2}$-$\sqrt{2}$t�����t=2-$\sqrt{2}$����ͼ4�У�����Bƽ�Ƶ�y����ʱ���ص��������ı���OA��MB����Գ�ͼ�Σ���ͼ5�У�����Bƽ�Ƶ�A��B����ʱ���ص������ǡ�A��BM�ǵ���ֱ�������Σ�����Գ�ͼ�Σ���ʱ��OM=BM���õ�$\sqrt{2}$��t-2$\sqrt{2}$��=$\sqrt{2}$-��t-2$\sqrt{2}$�������t=2+$\sqrt{2}$���ɴ˼��ɽ�����⣮
��� �⣺��1����ͼ1�У�
������A�䣨-1��-1����C�䣨2��-2������A�䣨-1��-1����C�䣨2��-2������y=ax2+bx��$\left\{\begin{array}{l}{a-b=-1}\\{4a+2b=-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{1}{3}}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{2}{3}$x2+$\frac{1}{3}$x��
��2����ͼ1�У�����A��C�䣬OB�佻�ڵ�E��
���ı���OA��B��C���Ǿ��Σ�
��A��E=EC�䣬OE=EB�䣬
��A�䣨-1��-1����C�䣨2��-2����
��E��$\frac{1}{2}$��-$\frac{3}{2}$����
��B�䣨1��-3����
��3����ͼ2�У���ֱ��PQ������OA��B��C��������Ϊ1��3�������֣�
��OP��PC��=1��3��OP�䣺P��C��=3��1��
�ٵ�OP��PC��=1��3ʱ��P��$\frac{1}{2}$��-$\frac{1}{2}$����
ֱ��PQ�Ľ���ʽΪy=x-1��
��$\left\{\begin{array}{l}{y=x-1}\\{y=-\frac{2}{3}{x}^{2}+\frac{1}{3}x}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{7}}{2}}\\{y=\frac{-3+\sqrt{7}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{-1-\sqrt{7}}{2}}\\{y=\frac{-3-\sqrt{7}}{2}}\end{array}\right.$��
�ߵ�Q�ڵ������ޣ�
��Q��$\frac{-1+\sqrt{7}}{2}$��$\frac{-3+\sqrt{7}}{2}$����
��D��0��-2����
��S��ODQ=$\frac{1}{2}$��2��$\frac{-1+\sqrt{7}}{2}$=$\frac{\sqrt{7}-1}{2}$��
�ڵ�OP�䣺P��C��=3��1ʱ��P�䣨$\frac{3}{2}$��-$\frac{3}{2}$����
��ֱ��P��Q��Ľ���ʽΪy=x-3��
��$\left\{\begin{array}{l}{y=x-3}\\{y=-\frac{2}{3}{x}^{2}+\frac{1}{3}x}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{19}}{2}}\\{y=\frac{-7+\sqrt{19}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{-1-\sqrt{19}}{2}}\\{y=\frac{-7-\sqrt{19}}{2}}\end{array}\right.$��
��Q�䣨$\frac{-1+\sqrt{19}}{2}$��$\frac{-7+\sqrt{19}}{2}$����
��S��ODQ��=$\frac{1}{2}$��2��$\frac{-1+\sqrt{19}}{2}$=$\frac{\sqrt{19}-1}{2}$��
��4����ͼ3�У�����Aƽ�Ƶ���A��B����ʱ���ص��������ı���AMON������Գ�ͼ�Σ���OM=AMʱ����ʱ$\sqrt{2}$t=$\sqrt{2}$-$\sqrt{2}$t�����t=2-$\sqrt{2}$��
��ͼ4�У�����Bƽ�Ƶ�y����ʱ���ص��������ı���OA��MB����Գ�ͼ�Σ���ʱt=2$\sqrt{2}$��

��ͼ5�У�����Bƽ�Ƶ�A��B����ʱ���ص������ǡ�A��BM�ǵ���ֱ�������Σ�����Գ�ͼ�Σ�
��ʱ��OM=BM���õ�$\sqrt{2}$��t-2$\sqrt{2}$��=$\sqrt{2}$-��t-2$\sqrt{2}$�������t=2+$\sqrt{2}$��
��������������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ����ʱ��t=2-$\sqrt{2}$��2$\sqrt{2}$��2+$\sqrt{2}$��t��2$\sqrt{2}$+1��
���� ���⿼����κ����ۺ��⡢���ε����ʡ������ε�������е����깫ʽ��ƽ�Ʊ任��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ��������ۣ�ѧ�ử��ͼ������ͼ�������⣬�����п�ѹ���⣮


| A�� | 4�� | B�� | 5�� | C�� | 6�� | D�� | 7�� |
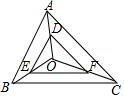 ��ͼ��O�ǡ�ABC������һ�㣬DE��AB��DF��AC��EF��BC����ô��ABC���DEF������˵�����ɣ�
��ͼ��O�ǡ�ABC������һ�㣬DE��AB��DF��AC��EF��BC����ô��ABC���DEF������˵�����ɣ�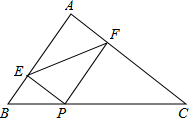 �ڡ�ABC�У�AB=6cm��AC=8cm��BC=10cm��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F������EF����EF����СֵΪ$\frac{24}{5}$cm��
�ڡ�ABC�У�AB=6cm��AC=8cm��BC=10cm��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F������EF����EF����СֵΪ$\frac{24}{5}$cm��