题目内容
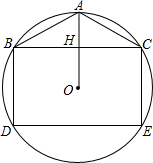 已知,如图,矩形BCED的两个顶点在⊙O上,过O作BC的垂线交BC于H,交⊙O于A,连AB,AC.
已知,如图,矩形BCED的两个顶点在⊙O上,过O作BC的垂线交BC于H,交⊙O于A,连AB,AC.(1)求证:AB=AC;
(2)若AB=BD=2,求⊙O的周长.
考点:垂径定理,勾股定理,矩形的性质
专题:
分析:(1)根据垂径定理即可证得;
(2)延长AO交⊙O于F,连接DF,从而证得四边形ABDF是等腰梯形,根据直径所对的圆周角是直角证得∠ABF=90°,然后通过等腰三角形和平行线的性质即可证得∠AFB=30°,根据30°所对的直角边等于斜边的一半即可求得直径,进而求得周长.
(2)延长AO交⊙O于F,连接DF,从而证得四边形ABDF是等腰梯形,根据直径所对的圆周角是直角证得∠ABF=90°,然后通过等腰三角形和平行线的性质即可证得∠AFB=30°,根据30°所对的直角边等于斜边的一半即可求得直径,进而求得周长.
解答:(1)证明:∵OA是⊙O的半径,OA⊥BC,
∴OA平分BC,
∴AB=AC;
(2)解:如图,延长AO交⊙O于F,连接DF,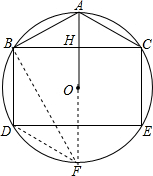
∵BD⊥BC,OA⊥BC,
∴BD∥AF,
∴DF=AB,∠DBF=∠BFA,
∵AB=BD=2,
∴AB=BD=DF=2,
∴四边形ABDF是等腰梯形,
∴∠BAF=∠DFA,
连接BF,
∵AF是直径,
∴∠ABF=90°,
∵BD=DF,
∴∠DBF=∠DFB,
∴∠DFB=∠AFB,
设∠DFB=∠AFB=∠DBF=x,
∴∠BAF=2x,
∵∠ABD+∠BAF=180°,
∴x+90°+2x=180°,解得x=30°,
∴∠AFB=30°,
∴AF=2AB=2×2=4,
∴⊙O的周长=4π.
∴OA平分BC,
∴AB=AC;
(2)解:如图,延长AO交⊙O于F,连接DF,

∵BD⊥BC,OA⊥BC,
∴BD∥AF,
∴DF=AB,∠DBF=∠BFA,
∵AB=BD=2,
∴AB=BD=DF=2,
∴四边形ABDF是等腰梯形,
∴∠BAF=∠DFA,
连接BF,
∵AF是直径,
∴∠ABF=90°,
∵BD=DF,
∴∠DBF=∠DFB,
∴∠DFB=∠AFB,
设∠DFB=∠AFB=∠DBF=x,
∴∠BAF=2x,
∵∠ABD+∠BAF=180°,
∴x+90°+2x=180°,解得x=30°,
∴∠AFB=30°,
∴AF=2AB=2×2=4,
∴⊙O的周长=4π.
点评:本题考查了垂径定理、直径所对的圆周角的性质,等腰梯形的判定和性质,平行线的性质以及30°所对的直角边等于斜边的一半的性质等,作出辅助线构建等腰梯形以及直角三角形是关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
邵华同学准备用6元钱买大小练习本若干本,已知大,小练习本单价分别为1元,0.5元,若任意选择一种方案购买,则恰好买到8本的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
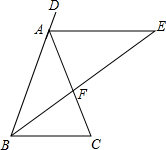 如图所示,在等腰△ABC中,AB=AC,∠BAC=36°,AE是△ABC的外角∠DAC的平分线,BF是∠ABC的平分线,BF的延长线交AE于E.
如图所示,在等腰△ABC中,AB=AC,∠BAC=36°,AE是△ABC的外角∠DAC的平分线,BF是∠ABC的平分线,BF的延长线交AE于E.
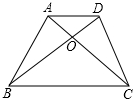 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,问:△AOB与△COD是否相似?
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,问:△AOB与△COD是否相似?