题目内容
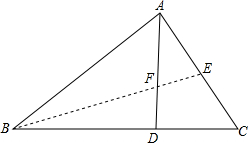如图，已知在△ABC中，D是BC上的一点，且BA2=BD•BC．（1）求证：△BDA∽△BAC；
（2）在图中画∠ABC的平分线，分别交边AC、AD于点E、F，求证：AE•AC=CE•AD．
考点：相似三角形的判定与性质
专题：证明题
分析：（1）由BA2=BD•BC可得
=
，且∠ABD=∠CBA，可证得△BDA∽△BAC；
（2）由角平分线的性质可得
=
，又由（1）△BDA∽△BAC可得
=
，可证得结论．
| AB |
| BC |
| BD |
| AB |
（2）由角平分线的性质可得
| AE |
| EC |
| AB |
| BC |
| AB |
| BC |
| AD |
| AC |
解答：证明：（1）∵BA2=BD•BC
∴
=
，且∠ABD=∠CBA，
∴△BDA∽△BAC；
（2）∵BE平分∠ABC，
∴
=
，
又由（1）△BDA∽△BAC可得
=
，
∴
=
，
∴AE•AC=CE•AD．
∴
| AB |
| BC |
| BD |
| AB |
∴△BDA∽△BAC；
（2）∵BE平分∠ABC，
∴
| AE |
| EC |
| AB |
| BC |
又由（1）△BDA∽△BAC可得
| AB |
| BC |
| AD |
| AC |
∴
| AE |
| EC |
| AD |
| AC |
∴AE•AC=CE•AD．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的判定方法及其性质是解题的关键，注意角平分线定理的应用．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
若（a-1）2+|b+2|=0，则|a+b|的值是（ ）
| A、3 | B、1 | C、2 | D、-121 |
如图所示，求阴影部分的周长．下列条件中，不能得到等边三角形的是（ ）
| A、有两个内角是60°的三角形 |
| B、三边都相等的三角形 |
| C、有一个角是60°的等腰三角形 |
| D、有两个外角相等的等腰三角形 |