题目内容
13.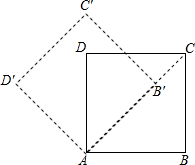 如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.
如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.
分析 根据正方形的性质得AC=$\sqrt{2}$(2+$\sqrt{2}$)=2$\sqrt{2}$+2,∠ACD=∠BAC=45°,再利用旋转的性质得∠BAB′=45°,AB′=AB=2+$\sqrt{2}$,∠AB′C′=∠B=90°,于是可判断点B′在AC上,所以CB′=AC-AB′=$\sqrt{2}$,然后利用△ECB′为等腰直角三角形易得CE=$\sqrt{2}$CB′=2.
解答  解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,
∴AC=$\sqrt{2}$(2+$\sqrt{2}$)=2$\sqrt{2}$+2,∠ACD=∠BAC=45°,
∵正方形ABCD绕点A逆时针方向旋转45°至正方形AB′C′D′,
∴∠BAB′=45°,AB′=AB=2+$\sqrt{2}$,∠AB′C′=∠B=90°,
∴点B′在AC上,
∴CB′=AC-AB′=2$\sqrt{2}$+2-2-$\sqrt{2}$=$\sqrt{2}$,
∵∠ECB′=45°,
∴△ECB′为等腰直角三角形,
∴CE=$\sqrt{2}$CB′=$\sqrt{2}$×$\sqrt{2}$=2.
故答案为2.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
相关题目
3.关于反比例函数y=$\frac{4}{x}$的图象,下列说法正确的是( )
| A. | 必经过点(2,-2) | B. | 两个分支分布在第二、四象限 | ||
| C. | 两个分支关于x轴成轴对称 | D. | 两个分支关于原点成中心对称 |
8.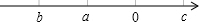 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )
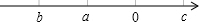 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )| A. | -c-2b | B. | a-2b-c | C. | -2a-c | D. | c |
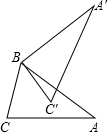 如图,在△ABC中,AB=AC,将△ABC绕点B逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′的度数为15°.
如图,在△ABC中,AB=AC,将△ABC绕点B逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′的度数为15°. 强强路交通拥堵,安全隐患严重,上周末,多多同学在强强人行天桥处对3000名过往行人作了问卷调查,问题是:从这里横过强强路时,你是否自觉走人行天桥,供选择的答案是:A、是;B、否;C、有时
强强路交通拥堵,安全隐患严重,上周末,多多同学在强强人行天桥处对3000名过往行人作了问卷调查,问题是:从这里横过强强路时,你是否自觉走人行天桥,供选择的答案是:A、是;B、否;C、有时
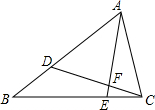 如图,已知△ABC,点D在边AB上,点E在边BC上,AE与CD交于点F.BD=4,AD=8,BE=6,CE=2.求EF:FC的值.
如图,已知△ABC,点D在边AB上,点E在边BC上,AE与CD交于点F.BD=4,AD=8,BE=6,CE=2.求EF:FC的值.