题目内容
4.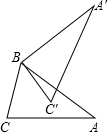 如图,在△ABC中,AB=AC,将△ABC绕点B逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′的度数为15°.
如图,在△ABC中,AB=AC,将△ABC绕点B逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′的度数为15°.
分析 先根据旋转的性质得∠ABA′=∠CBC′=60°,∠A=∠A′,再由A′C′⊥AB,则根据互余可计算出∠A′=30°,则∠A=30°,接着根据等腰三角形的性质和三角形内角和定理计算出∠ABC=∠C=75°,然后计算∠ABC-∠CBC′即可.
解答 解:∵△ABC绕点B逆时针方向旋转60°得到△A′BC′,
∴∠ABA′=∠CBC′=60°,∠A=∠A′,
∵A′C′⊥AB,
∴∠A′=90°-60°=30°,
∴∠A=30°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-30°)=75°,
∴∠ABC′=∠ABC-∠CBC′=75°-60°=15°.
故答案为15°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列说法正确的是( )
| A. | 有公共顶点的两个角是对顶角 | B. | 相等的角是对顶角 | ||
| C. | 有公共顶点且相等的角是对顶角 | D. | 对顶角相等 |
12.若方程组$\left\{\begin{array}{l}{x+y=3}\\{2x+y=□}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=□}\end{array}\right.$,则前后两个□的数分别是( )
| A. | 4,2 | B. | 1,3 | C. | 2,3 | D. | 5,2 |
14.直角三角形的外心在( )
| A. | 直角顶点 | B. | 直角三角形内 | C. | 直角三角形外 | D. | 斜边中点 |
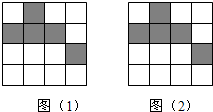 如图(1)、(2)分别是由16个小正方形组成的正方形网格图,现已将其中部分小正方形涂黑,请你用两种不同的方法,分别在两个图中再涂黑两个空白的小正方形,使它(涂黑部分)成为轴对称图形.
如图(1)、(2)分别是由16个小正方形组成的正方形网格图,现已将其中部分小正方形涂黑,请你用两种不同的方法,分别在两个图中再涂黑两个空白的小正方形,使它(涂黑部分)成为轴对称图形.
 如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为x>-2.
如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为x>-2.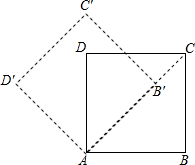 如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.
如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.