题目内容
2.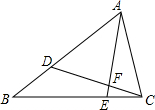 如图,已知△ABC,点D在边AB上,点E在边BC上,AE与CD交于点F.BD=4,AD=8,BE=6,CE=2.求EF:FC的值.
如图,已知△ABC,点D在边AB上,点E在边BC上,AE与CD交于点F.BD=4,AD=8,BE=6,CE=2.求EF:FC的值.
分析 根据已知条件得到$\frac{AB}{BC}=\frac{BE}{BD}$,由于∠B=∠B,推出△ABE∽△CBD,于是得到$\frac{AE}{CD}$=$\frac{3}{2}$求得△AFD∽△CFE求出EF=$\frac{1}{5}$AE,同理CF=$\frac{1}{5}$CD,于是得到结论.
解答 解:∵$\frac{AB}{BC}=\frac{12}{8}=\frac{3}{2}$,$\frac{BE}{BD}=\frac{6}{4}=\frac{3}{2}$,
∴$\frac{AB}{BC}=\frac{BE}{BD}$,
∵∠B=∠B,
∴△ABE∽△CBD,
∴$\frac{AE}{CD}$=$\frac{3}{2}$,
∵∠BAE=∠BCD,∠AFD=∠CFE,
∴△AFD∽△CFE,
∴$\frac{AD}{CE}=\frac{8}{2}=4$,
∴$\frac{EF}{AF}=\frac{1}{4}$,
∴EF=$\frac{1}{5}$AE,同理CF=$\frac{1}{5}$CD,
∴EF:CF=$\frac{1}{5}$AE:$\frac{1}{5}$CD=AE:CD=2:3.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
12.若方程组$\left\{\begin{array}{l}{x+y=3}\\{2x+y=□}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=□}\end{array}\right.$,则前后两个□的数分别是( )
| A. | 4,2 | B. | 1,3 | C. | 2,3 | D. | 5,2 |
10.某步行街一商店将某种服装按成本提高40%标价,为了吸引顾客,在十一期间又以8折优惠卖出,结果每件服装仍可获利15元,则这种服装每件的成本为( )
| A. | 140元 | B. | 135元 | C. | 125元 | D. | 120元 |
7.学业考试体育测试结束后,某班体育委员将本班50名学生的测试成绩制成如下的统计表.这个班学生体育测试成绩的众数是( )
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 1 | 2 | 4 | 5 | 6 | 5 | 8 | 10 | 6 | 2 |
| A. | 30分 | B. | 28分 | C. | 25分 | D. | 10人 |
14.直角三角形的外心在( )
| A. | 直角顶点 | B. | 直角三角形内 | C. | 直角三角形外 | D. | 斜边中点 |
11.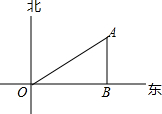 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60°方向500m处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60°方向500m处,那么水塔所在的位置到公路的距离AB是( )
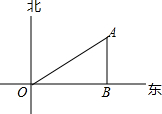 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60°方向500m处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60°方向500m处,那么水塔所在的位置到公路的距离AB是( )| A. | 250m | B. | 250$\sqrt{3}$m | C. | $\frac{500}{3}$$\sqrt{3}$m | D. | 250$\sqrt{2}$m |
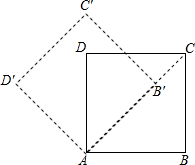 如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.
如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.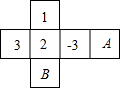 如图,是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和-3在其余正方形内分别填上A和B,使得折成正方体后,相对面上的两数互为相反数,则A+B的值是-3.
如图,是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和-3在其余正方形内分别填上A和B,使得折成正方体后,相对面上的两数互为相反数,则A+B的值是-3.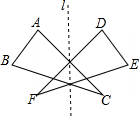 如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.
如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.