题目内容
18.如图数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
(1)表中第9行的最后一个数是81,它是自然数9的平方,第9行共有17个数;
(2)表中第(n+1)行的第一个数是n2+1,最后一个数是(n+1)2,第(n+1)行共有2n+1个数;(用含n的代数式表示)
(3)求第(n+1)行各数之和.
分析 (1)第1行最后一个数为12,第2行最后一个数为22,第3行最后一个数为32,第4行最后一个数为42,…第9行最后一个数为92,共有92-82个数;
(2)由(1)知第n+1行最后一数为(n+1)2,则第一个数为n2+1,该行共有(n+1)2-n2个数;
(3)通过(2)的结果列式从而解得结果.
解答 解:(1)∵第1行最后一个数为12,第2行最后一个数为22,第3行最后一个数为32,第4行最后一个数为42,…
∴第9行最后一个数为92=81,它是自然数9的平方,共有92-82=17个数,
故答案为:81,9,17;
(2)由(1)知第(n+1)行的第一个数是n2+1,
最后一个数是(n+1)2,
共有(n+1)2-n2=2n+1个数,
故答案为:n2+1,(n+1)2,2n+1;
(3)第(n+1)行各数之和等于${\frac{1}{2}×[n}^{2}+1+(n+1)^{2}]×(2n+1)$=(2n+1)(n2+n+1)=2n3+3n2+3n+1.
点评 本题主要考查了数字的变化规律,发现每行末尾数字是行数的平方是解答此题的关键.

练习册系列答案
相关题目
3.某公司全体员工年薪的具体情况如表:
则所有员工的年薪平均数比中位数多2万元.
| 年薪/万元 | 30 | 14 | 9 | 6 | 4 | 3.5 |
| 员工数/人 | 1 | 1 | 1 | 2 | 7 | 6 |
10.某步行街一商店将某种服装按成本提高40%标价,为了吸引顾客,在十一期间又以8折优惠卖出,结果每件服装仍可获利15元,则这种服装每件的成本为( )
| A. | 140元 | B. | 135元 | C. | 125元 | D. | 120元 |
7.学业考试体育测试结束后,某班体育委员将本班50名学生的测试成绩制成如下的统计表.这个班学生体育测试成绩的众数是( )
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 1 | 2 | 4 | 5 | 6 | 5 | 8 | 10 | 6 | 2 |
| A. | 30分 | B. | 28分 | C. | 25分 | D. | 10人 |
 如图,C为射线BM上一点,CF是∠ACM的平分线,且CF∥AB,∠B=50°,求∠FCM、∠FCA、∠A的度数.
如图,C为射线BM上一点,CF是∠ACM的平分线,且CF∥AB,∠B=50°,求∠FCM、∠FCA、∠A的度数.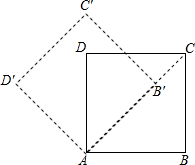 如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.
如图,将边长为$2+\sqrt{2}$的正方形ABCD绕点A逆时针方向旋转45°至AB′C′D′,若CD和B′C′相交于点E,则CE=2.