题目内容
1.(1)解不等式2(4x-3)≤15x-20,并把解集在数轴上表示出来.(2)解不等式组$\left\{\begin{array}{l}{5x-3>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$.
分析 (1)去分母、去括号、移项、合并同类项、系数华晨1即可求解;
(2)首先解每个不等式,两个不等式解集的公共部分就是不等式组的解集.
解答 解:(1)去括号,得8x-6≤15x-20,
移项,得8x-15x≤-20+6,
合并同类项,得-7x≤-14,
系数化成1得x≥2. ;
;
(2)$\left\{\begin{array}{l}{5x-3>3(x-1)…①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x…②}\end{array}\right.$,
解①得:x>0,
解②得:x≤4. ,
,
不等式组的解集是:0<x≤4.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
6.在平面直角坐标系中,把点A(x,1)向上平移4个单位长度,再向右平移3个单位长度得到点B(-2,y),则x和y的值分别为( )
| A. | -6,-4 | B. | -1,5 | C. | -5,3 | D. | -5,5 |
10.已知2a-y+5b3x与-5a2xb2+4y是同类项,则( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$ |
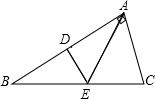 在Rt△ABC,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连结AE,则△ACE的周长是( )
在Rt△ABC,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连结AE,则△ACE的周长是( )