题目内容
17．已知三角形的各边长分别为8cm，10cm和12cm，求以各边中点为顶点的三角形的周长．分析 由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半，即可求其周长．
解答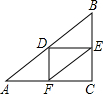 
解：如图，D，E，F分别是△ABC的三边的中点，
则DE=$\frac{1}{2}$AC，DF=$\frac{1}{2}$BC，EF=$\frac{1}{2}$AB，
∴△DEF的周长=DE+DF+EF=$\frac{1}{2}$（AC+BC+AB）=$\frac{1}{2}$×（8+10+12）cm=15cm．
答：以各边中点为顶点的三角形的周长是15cm．
点评 本题考查了三角形中位线定理．解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系．
练习册系列答案
相关题目
8．吉州区为推动教育优质均衡发展，发挥教育公平的基础性作用，近几年来共投入了教育经费10亿元，用科学记数法表示10亿为（ ）
| A． | 10×108 | B． | 0.1×1010 | C． | 1×109 | D． | 1×1010 |
5．
学校举行“文明环保，从我做起”征文比赛．现有甲班上交40篇作文，乙班上交30篇作文，现将两班的作文的成绩（单位：分）统计如下：
甲班：
根据上面提供的信息回答下列问题
（1）表中x=3，甲班学生成绩的中位数落在等级C中，扇形统计图中等级D部分的扇形圆心角n=36°．
（2）现学校决定从两班所有A等级成绩的学生中随机抽取2名同学参加市级征文比赛．求抽取到两名学生恰好来自同一班级的概率（请列表求解）．
学校举行“文明环保，从我做起”征文比赛．现有甲班上交40篇作文，乙班上交30篇作文，现将两班的作文的成绩（单位：分）统计如下：甲班：
| 等级 | 成绩（S） | 频数 |
| A | 90＜S≤100 | x |
| B | 80＜S≤90 | 16 |
| C | 70＜S≤80 | 18 |
| D | S≤70 | 3 |
| 合计 | 40 |
（1）表中x=3，甲班学生成绩的中位数落在等级C中，扇形统计图中等级D部分的扇形圆心角n=36°．
（2）现学校决定从两班所有A等级成绩的学生中随机抽取2名同学参加市级征文比赛．求抽取到两名学生恰好来自同一班级的概率（请列表求解）．
12．下列几何体中，同一个几何体的主视图与左视图不同的是（ ）
| A． |  圆柱 | B． |  正方体 | C． |  圆锥 | D． |  球 |
2．
如图所示的几何体的俯视图是（ ）
如图所示的几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
9．若代数式$\frac{1}{x-9}$有意义，则实数x的取值范围是（ ）
| A． | x≠0 | B． | x≥0 | C． | x≠9 | D． | x≥9 |
6．在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，先从中随机摸出一个小球，再从余下的球中随机摸出一个小球，第二次摸出的小球的标号是第一次的整数倍的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{6}$ |
7．估计$\sqrt{16}$×2-$\sqrt{2}$的运算结果在哪两个相邻的整数之间（ ）
| A． | 4和5 | B． | 5和6 | C． | 6和7 | D． | 7和8 |