题目内容
不能进行密铺的图形是( )
| A、正三边形 | B、正四边形 |
| C、正五边形 | D、正六边形 |
考点:平面镶嵌(密铺)
专题:
分析:几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.360°为正多边形一个内角的整数倍才能单独镶嵌.
解答:解:A、正三边形的一个内角度数为180-360÷3=60°,是360°的约数,能镶嵌平面,不符合题意;
B、正四边形形的一个内角度数为180-360÷4=90°,是360°的约数,能镶嵌平面,不符合题意;
C、正五边形的一个内角度数为180-360÷5=108°,不是360°的约数,不能镶嵌平面,符合题意;
D、正六边形的一个内角度数为180-360÷6=120°,是360°的约数,能镶嵌平面,不符合题意.
故选C.
B、正四边形形的一个内角度数为180-360÷4=90°,是360°的约数,能镶嵌平面,不符合题意;
C、正五边形的一个内角度数为180-360÷5=108°,不是360°的约数,不能镶嵌平面,符合题意;
D、正六边形的一个内角度数为180-360÷6=120°,是360°的约数,能镶嵌平面,不符合题意.
故选C.
点评:本题考查了平面密铺的知识,注意掌握只用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.

练习册系列答案
相关题目
关于x的方程x2+2kx+k-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都有实根 |
| B、k为任何实数,方程都有两个不相等的实根 |
| C、k为任何实数,方程都有两个相等的实根 |
| D、以上说法都对 |
 如图,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为( )
如图,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为( )| A、5 | B、6 | C、7 | D、不确定 |
在实数:9-
,0.666,
,
,
,5.2121121112…(每两个2之间依次多一个1)中,无理数的个数有( )
| 9 |
| 3 | 125 |
| 3 | -6 |
| 22 |
| 7 |
| A、1个 | B、2个 | C、3个 | D、4个 |
计算(2+1)(22+1)(24+1)(28+1)得( )
| A、28-1 |
| B、210-1 |
| C、216-1 |
| D、232-1 |
2.796精确到百分位的结果是( )
| A、2.79 | B、2.81 |
| C、2.7 | D、2.80 |
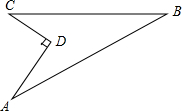 如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?