题目内容
4.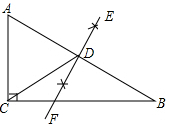 如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )| A. | 13 | B. | 17 | C. | 18 | D. | 25 |
分析 利用勾股定理可得AB的长,然后根据题意可得EF是AB的垂直平分线,进而可得AD的长和CD的长,进而可得答案.
解答 解:∵∠ACB=90°,BC=12,AC=5,
∴AB=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
根据题意可得EF是AB的垂直平分线,
∴D是AB的中点,
∴AD=$\frac{1}{2}$AB=6.5,CD=$\frac{1}{2}$AB=6.5,
∴△ACD的周长为:13+5=18,
故选:C.
点评 此题主要考查了勾股定理和线段垂直平分线的性质,关键是掌握勾股定理和线段垂直平分线的作法.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
19.-7的绝对值是( )
| A. | -7 | B. | 7 | C. | ±7 | D. | $\frac{1}{7}$ |
9.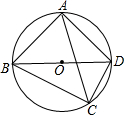 已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
 已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )| A. | AC=BC+CD | B. | $\sqrt{2}$AC=BC+CD | C. | $\sqrt{3}$AC=BC+CD | D. | 2AC=BC+CD |
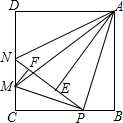 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.
如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA. 如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.