题目内容
13.已知9m=$\frac{3}{2}$,3n=$\frac{1}{2}$,则下列结论正确的是( )| A. | 2m-n=1 | B. | 2m-n=3 | C. | 2m+n=3 | D. | 2m=3n |
分析 根据同底数幂的除法,可得答案.
解答 解:9m÷3n=32m-n=$\frac{3}{2}$÷$\frac{1}{2}$=3,
2m-n=1,
故选:A.
点评 本题考查了同底数幂的除法,利用同底数幂的除法是解题关键.

练习册系列答案
相关题目
8.问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢?
问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
(2)在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
则S与a,b之间的关系为S=a+2b-2(用含a,b的代数式表示).

问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1(图3) | 8 | 1 | 8 |
| 多边形2(图4) | 7 | 3 | 11 |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
2.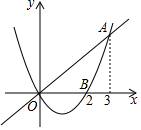 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>3 | C. | 2<x<3 | D. | 0<x<3 |
 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E. 已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=4,CD=4,AD=6,求四边形ABCD的面积.
已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=4,CD=4,AD=6,求四边形ABCD的面积. 如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是108°.
如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是108°.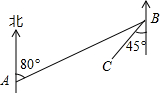 一艘轮船从点A出发沿北偏东80°,方向航行到点B后再沿西南方向航行,则∠ABC=35°.
一艘轮船从点A出发沿北偏东80°,方向航行到点B后再沿西南方向航行,则∠ABC=35°.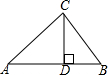 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?