题目内容
3.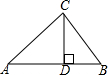 某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水果的造价为30元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
分析 当CD为斜边上的高时,CD最短,从而水渠造价最低,根据已知条件可将CD的长求出,在Rt△ACD中运用勾股定理求出AD的长,进而可得出结论.
解答 解:当CD为斜边上的高时,CD最短,从而水渠造价最低,
∵∠ACB=90°,AC=80米,BC=60米,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{8{0}^{2}+6{0}^{2}}$=100米,
∵CD•AB=AC•BC,即CD•100=80×60,
∴CD=48米,
∴在Rt△ACD中AC=80,CD=48,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{8{0}^{2}-4{8}^{2}}$=64米,48×30=1440元.
所以,D点在距A点64米的地方,水渠的造价最低,其最低造价为1440元.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
13.已知9m=$\frac{3}{2}$,3n=$\frac{1}{2}$,则下列结论正确的是( )
| A. | 2m-n=1 | B. | 2m-n=3 | C. | 2m+n=3 | D. | 2m=3n |
18.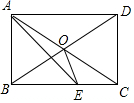 在矩形ABCD中,AC和BD交于点O,∠AOB=60°,AE平分∠BAD交BC于E,则∠BOE的度数为( )
在矩形ABCD中,AC和BD交于点O,∠AOB=60°,AE平分∠BAD交BC于E,则∠BOE的度数为( )
 在矩形ABCD中,AC和BD交于点O,∠AOB=60°,AE平分∠BAD交BC于E,则∠BOE的度数为( )
在矩形ABCD中,AC和BD交于点O,∠AOB=60°,AE平分∠BAD交BC于E,则∠BOE的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
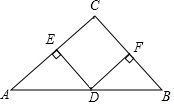 如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E,F,求证:四边形CEDF是正方形.
如图,△ABC中,∠C=90°,AC=BC,点D是AB的中点,分别过点D作DE⊥AC,DF⊥BC,垂足分别为点E,F,求证:四边形CEDF是正方形.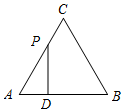 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )
如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )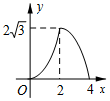
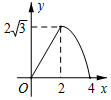
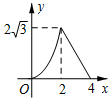
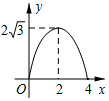
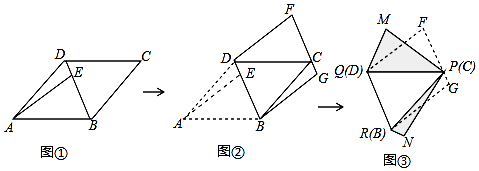
 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB、∠DCB、∠EDC的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB、∠DCB、∠EDC的度数. 如图,在5×5的网格中,每个小正方形的边长都是1个单位长度,网格中小正方形的顶点叫做格点,矩形ABCD的边分别过格点E,F,G,H,则OD的最大值为6.
如图,在5×5的网格中,每个小正方形的边长都是1个单位长度,网格中小正方形的顶点叫做格点,矩形ABCD的边分别过格点E,F,G,H,则OD的最大值为6.