题目内容
9.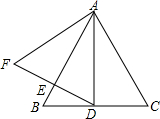 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )| A. | 30° | B. | 35° | C. | 55° | D. | 60° |
分析 根据等腰三角形的性质得到∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}×$70°=35°,根据线段垂直平分线的性质得到AF=AD,即可得到结论.
解答 解:∵AB=AC,D是BC中点,
∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}×$70°=35°,
∵DE⊥AB,
∴∠ADE=55°,
∵EF=DE,DE⊥AB,
∴AF=AD,
∴∠F=∠ADE=55°.
故选:C.
点评 本题考查了等腰三角形的判定和性质,线段的垂直平分线的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
19.已知一元二次方程ax2+bx+c=0的一个根是x1=0,二次函数y=ax2+bx+c关于直线x=1对称,则方程的另一根为( )
| A. | x2=0 | B. | x2=1 | C. | x2=-2 | D. | x2=2 |
17.若关于x的分式方程$\frac{x-m}{x-1}-\frac{3}{x}$=1无解,则m的值为( )
| A. | 0 | B. | 1 | C. | -2 | D. | 1或-2 |
4.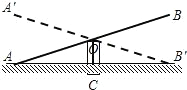 如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
 如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )| A. | 40° | B. | 60° | C. | 80° | D. | 20° |
14.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2015的坐标为( )
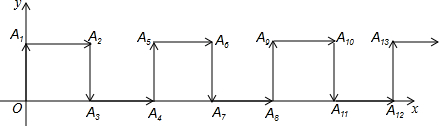

| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
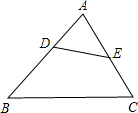 如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.
如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.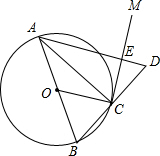 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.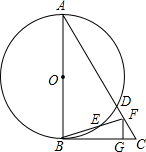 如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.