题目内容
18.在△ABC中,AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD=2或$\frac{5}{3}$cm.分析 由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
解答 解:∵S△ADE:S四边形BCED=1:8,
∴S△ADE:S△ABC=1:9,
∴△ADE与△ABC相似比为:1:3,
①若∠AED对应∠B时,
则$\frac{AD}{AC}=\frac{1}{3}$,
∵AC=5cm,
∴AD=$\frac{5}{3}$cm;
②当∠ADE对应∠B时,则$\frac{AD}{AB}=\frac{1}{3}$,
∵AB=6cm,
∴AD=2cm;
故答案为:$2或\frac{5}{3}$.
点评 本题考查的是相似三角形的性质,相似三角形的对应边成比例,相似三角形的面积比等于相似比的平方,意识到有两种情况分类讨论是解决问题的关键.

练习册系列答案
相关题目
8.某商场为从甲、乙两种电子钟中购入一种去销售.从两种电子钟中各随机取10台进行测试,两种电子钟走时误差的数据如下表.(单位:秒)
(1)计算出甲、乙两种电子钟走时误差的平均数;
(2)计算出甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,消费者也更愿意购买.若销售一台甲种电子钟和销售一台乙种电子钟的利润相同,请问:商场应购入哪种电子钟去销售,为什么?
类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(2)计算出甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,消费者也更愿意购买.若销售一台甲种电子钟和销售一台乙种电子钟的利润相同,请问:商场应购入哪种电子钟去销售,为什么?
9.当代数式x2+3x+8的值等于7时,代数式3x2+9x-2的值等于( )
| A. | 5 | B. | 3 | C. | -2 | D. | -5 |
 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )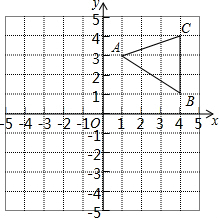 如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4). 如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.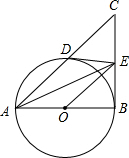 如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE
如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE 已知:△ABC.
已知:△ABC.