题目内容
20.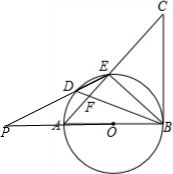 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF•DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径.
分析 (1)根据圆周角定理即可得出∠EAB+∠EBA=90°,再由已知得出∠ABE+∠CBE=90°,则CB⊥AB,从而证得BC是⊙O的切线;
(2)通过证得△DEF∽△DBE,得出相似三角形的对应边成比例即可证得结论.
(3)连接DA、DO,先证得OD∥BE,得出$\frac{PD}{PE}$=$\frac{PO}{PB}$,然后根据已知条件得出$\frac{PO}{PB}$=$\frac{PD}{PE}$=$\frac{PD}{PD+DE}$=$\frac{2}{3}$,求得PD=4,通过证得△PDA∽△POD,得出$\frac{PD}{PO}$=$\frac{PA}{PD}$,设OA=x,则PA=x,PO=2x,得出$\frac{4}{2x}$=$\frac{x}{4}$,解得OA=2$\sqrt{2}$.
解答 (1)证明:∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∵∠EDB=∠EAB,∠BDE=∠CBE,
∴∠EAB=∠CBE,
∴∠ABE+∠CBE=90°,
∴CB⊥AB,
∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)证明:∵BD平分∠ABE,
∴∠ABD=∠DBE,$\widehat{AD}$=$\widehat{DE}$,
∴∠DEA=∠DBE,
∵∠EDB=∠BDE,
∴△DEF∽△DBE,
∴$\frac{DE}{DB}$=$\frac{DF}{DE}$,
∴DE2=DF•DB;
(3) 解:连接DA、DO,
解:连接DA、DO,
∵OD=OB,
∴∠ODB=∠OBD,
∵∠EBD=∠OBD,
∴∠EBD=∠ODB,
∴OD∥BE,
∴$\frac{PD}{PE}$=$\frac{PO}{PB}$,
∵PA=AO,
∴PA=AO=OB,
∴$\frac{PO}{PB}$=$\frac{2}{3}$
∴$\frac{PD}{PE}$=$\frac{2}{3}$,
∴$\frac{PD}{PD+DE}$=$\frac{2}{3}$,
∵DE=2,
∴PD=4,
∵∠PDA+∠ADE=180°,∠ABE+∠ADE=180°,
∴∠PDA=∠ABE,
∵OD∥BE,
∴∠AOD=∠ABE,
∴∠PDA=∠AOD,
∵∠P=∠P,
∴△PDA∽△POD,
∴$\frac{PD}{PO}$=$\frac{PA}{PD}$,
设OA=x,
∴PA=x,PO=2x,
∴$\frac{4}{2x}$=$\frac{x}{4}$,
∴2x2=16,x=2$\sqrt{2}$,
∴OA=2$\sqrt{2}$.
点评 本题考查了切线的判定,三角形相似的判定和性质;要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

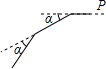 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(2)计算出甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,消费者也更愿意购买.若销售一台甲种电子钟和销售一台乙种电子钟的利润相同,请问:商场应购入哪种电子钟去销售,为什么?
| A. | 5 | B. | 3 | C. | -2 | D. | -5 |
 如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2=34°.
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2=34°.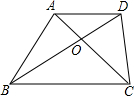 如图,梯形ABCD中,AD∥BC,AB⊥AC,AB=AC,BD=BC,若AD=$\sqrt{2}$,则梯形的面积是$\frac{5+3\sqrt{3}}{2}$.
如图,梯形ABCD中,AD∥BC,AB⊥AC,AB=AC,BD=BC,若AD=$\sqrt{2}$,则梯形的面积是$\frac{5+3\sqrt{3}}{2}$.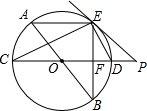 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )