题目内容
4. 如图,矩形EFGH内接于△ABC,且边FG落在BC上,若BC=5,AD=4,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{30}{11}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上,若BC=5,AD=4,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{30}{11}$.
分析 设EH=3x,表示出EF,由AD-EF表示出三角形AEH的边EH上的高,根据三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,即为EH的长.
解答 解:∵四边形EFGH是矩形,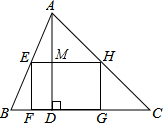
∴EH∥BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴$\frac{AM}{AD}=\frac{EH}{BC}$,
设EH=3x,则有EF=2x,AM=AD-EF=4-2x,
∴$\frac{4-2x}{4}$=$\frac{3x}{5}$,
解得:x=$\frac{10}{11}$,
则EH=$\frac{30}{11}$.
故答案为:$\frac{30}{11}$.
点评 此题考查了相似三角形的判定与性质,以及矩形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列属于定义的是( )
| A. | 两点确定一条直线 | |
| B. | 线段是直线上的两点和两点间的部分 | |
| C. | 同角或等角的补角相等 | |
| D. | 内错角相等,两直线平行 |
16.下列由四舍五入得到的近似数精确到千位的是( )
| A. | 2.8×104 | B. | 0.021 | C. | 6318 | D. | 3.12万 |
14.已知两圆的半径分别为一元二次方程x2-7x+12=0的二根,圆心距为1,则两圆位置关系为( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 相离 |
 如图,直角三角形纸片ACB,∠ACB=90°,AB=5,AC=3,将其折叠,使点C落在斜边上的点C′,折痕为AD;再沿DE折叠,使点B落在DC′的延长线上的点B′处.
如图,直角三角形纸片ACB,∠ACB=90°,AB=5,AC=3,将其折叠,使点C落在斜边上的点C′,折痕为AD;再沿DE折叠,使点B落在DC′的延长线上的点B′处. 如图,有一块长和宽分别为70厘米和50厘米的长方形铁皮,要在它的四角截去四个全等的小正方形,做成一个无盖的长方体铁盒,且使盒子的底面积为1500平方厘米,那么做成盒子的高是多少厘米?
如图,有一块长和宽分别为70厘米和50厘米的长方形铁皮,要在它的四角截去四个全等的小正方形,做成一个无盖的长方体铁盒,且使盒子的底面积为1500平方厘米,那么做成盒子的高是多少厘米?