题目内容
 某村在村口建可有个如图所示的牌门,牌门上部是圆弧AD,已知牌门的宽BC为4m,立柱BC,CD高为2m,弧AD的中点E与BC距离为3m.
某村在村口建可有个如图所示的牌门,牌门上部是圆弧AD,已知牌门的宽BC为4m,立柱BC,CD高为2m,弧AD的中点E与BC距离为3m.(1)求圆弧AD的半径;
(2)现在有一辆宽3m,高2.4m的大货车要经过,它能通过吗?
考点:垂径定理的应用,勾股定理
专题:
分析:(1)设圆弧AD的半径为R,则OD=R,EF=EG-DC=1m,OF=(R-1)m,由垂径定理求出DF=AF=
AD=2m,在Rt△OFD中,由勾股定理得出方程R2=(R-1)2+22,求出即可;
(2)先根据题意画出图形,根据已知求出EH=0.6m,垂径定理求出HW,求出OH,求出此时HE的长,再比较即可.
| 1 |
| 2 |
(2)先根据题意画出图形,根据已知求出EH=0.6m,垂径定理求出HW,求出OH,求出此时HE的长,再比较即可.
解答:解:(1)设圆弧AD的半径为R,则OD=R,EF=EG-DC=3m-2m=1m,OF=(R-1)m,
由垂径定理得:DF=AF=
AD,
∵AD=BC=4m,
∴DF=2m,
在Rt△OFD中,由勾股定理得:R2=(R-1)2+22,
解得:R=2.5,
即圆弧AD的半径为2.5m;
(2)
答:它能通过,
理由是:如图,加入车的平面图形为矩形QRPW,QW交OE于H,
则由垂径定理得:QH=HW=
×3m=1.5m,
在Rt△OHW中,由勾股定理得:OH=
=2(m),
∵半径OE=2.5m,OH=2m,
∴HE=0.5m,
∵GH=2.4,EG=3m,
∴OG=2.4-2=0.4,
∴HE=3m-2.4m=0.6m,
∴0.6>0.5,
∴一辆宽3m,高2.4m的大货车要经过,它能通过.
由垂径定理得:DF=AF=
| 1 |
| 2 |
∵AD=BC=4m,
∴DF=2m,
在Rt△OFD中,由勾股定理得:R2=(R-1)2+22,
解得:R=2.5,
即圆弧AD的半径为2.5m;
(2)

答:它能通过,
理由是:如图,加入车的平面图形为矩形QRPW,QW交OE于H,
则由垂径定理得:QH=HW=
| 1 |
| 2 |
在Rt△OHW中,由勾股定理得:OH=
| 2.52-1.52 |
∵半径OE=2.5m,OH=2m,
∴HE=0.5m,
∵GH=2.4,EG=3m,
∴OG=2.4-2=0.4,
∴HE=3m-2.4m=0.6m,
∴0.6>0.5,
∴一辆宽3m,高2.4m的大货车要经过,它能通过.
点评:本题考查了垂径定理,勾股定理等知识点的应用,解此题的关键是能求出圆的半径,题目比较典型,难度适中.

练习册系列答案
相关题目
 如下图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A、B是数轴上的点,完成下列各题:
如下图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A、B是数轴上的点,完成下列各题: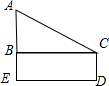 Rt△ABC中,∠ABC=90°,∠ACB=30°,四边形BCDE为矩形,且CD=
Rt△ABC中,∠ABC=90°,∠ACB=30°,四边形BCDE为矩形,且CD= 作图题(保留作图痕迹,不写作法).
作图题(保留作图痕迹,不写作法). 如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.
如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD. 如图,以矩形ABDE的一边BD为直径作半圆O,BE交圆O于C,AC的延长线交ED于M,交BD的延长线于N,若ME=MC.
如图,以矩形ABDE的一边BD为直径作半圆O,BE交圆O于C,AC的延长线交ED于M,交BD的延长线于N,若ME=MC. 矩形ABCD的长AD=a,宽AB=b,E、F分别是AD、BC 上的点,BE、DF是相距为h的平行线,求AE的长(用a、b、h表示).
矩形ABCD的长AD=a,宽AB=b,E、F分别是AD、BC 上的点,BE、DF是相距为h的平行线,求AE的长(用a、b、h表示). 如图,五边形ABCDE内接于⊙O,且AB=BC=CD=DE=AE,BD和CE相交于F,求证:四边形ABFE是菱形.
如图,五边形ABCDE内接于⊙O,且AB=BC=CD=DE=AE,BD和CE相交于F,求证:四边形ABFE是菱形.