题目内容
1.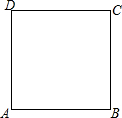 如图,边长为2的正方形ABCD,一点P从A点出发沿AB-BC以每秒1个单位速度运动到C点,设运动的时间为x秒,四边形APCD的面积为y.
如图,边长为2的正方形ABCD,一点P从A点出发沿AB-BC以每秒1个单位速度运动到C点,设运动的时间为x秒,四边形APCD的面积为y.(1)写出y与x之间的函数关系式及x的取值范围;
(2)说明是否存在时间x,使四边形APCD的面积为2.5?
分析 (1)分成当P在AB上时,即0<x≤2时和当P在BC上时,2<x≤4时两种情况进行讨论,利用梯形的面积公式求解;
(2)分两种情况令y=2.5,求解x即可.
解答 解:(1)当P在AB上时,即0<x≤2时,y=$\frac{1}{2}$AD(AP+CD)=$\frac{1}{2}$×2×(2+x),即y=2+x;
当P在BC上时,2<x≤4时,y=$\frac{1}{2}$CD•(AD+CP)=$\frac{1}{2}$×2×(2+4-x),即y=6-x;
(2)当0<x≤2时,y=2+x=2.5,解得x=0.5;
当2<x≤4时,y=6-x=2.5,解得x=3.5.
点评 本题考查了函数关系式,正确分两种情况讨论,利用x表示出AP和CP的长是关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
11.在等腰直角三角形所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形,这样的点一共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程y(千米)与行驶时间x(小时)之间的函数关系式是( )
| A. | y=80x-100 | B. | y=-80x-100 | C. | y=80x+100 | D. | y=-80x+100 |
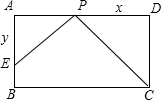 已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE⊥CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE⊥CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并写出x的取值范围. 请找出图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.
请找出图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.