题目内容
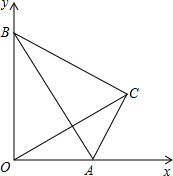 如图,在直角坐标系中,一个Rt△ABC的斜边AB在两坐标轴上滑动,AB=2,∠ABC=30°,下面说法正确的个数是( )个.
如图,在直角坐标系中,一个Rt△ABC的斜边AB在两坐标轴上滑动,AB=2,∠ABC=30°,下面说法正确的个数是( )个.①当B点与O点重合时,C点的坐标是(
| 3 |
| 2 |
| ||
| 2 |
②滑动过程中,OC的最大值是2;
③滑动过程中,四边形OACB的面积的最大值是1+
| ||
| 2 |
④滑动过程中,AB的中点所走的路径是一条线段.
| A、1 | B、2 | C、3 | D、4 |
考点:圆的综合题
专题:
分析:根据解直角三角形的运用、四点共圆的性质、三角形的内角和定理、三角形的面积公式以及二次函数的性质逐项分析即可.
解答:解:由解直角三角形知①正确;
取AB的中点D,(如图1)连OD、CD,则CO≤OC+OD(当O、D、C三点共线时取等号),此时OC=AB=2,知②正确;
(另外也可以这样考虑,如图2,∠AOB=∠ACB=90°,则∠AOB+∠ACB=180°,O、A、C、B四点共圆,OC为⊙D的弦,OC≤AB=2,当OC为⊙D的 直径时,OC最大是2,也得结论②正确;
直径时,OC最大是2,也得结论②正确;
由于△ABC的面积是
×1×
=
(定值),当△AOB面积最大时,四边形的面积最大,当△AOB是等腰直角三角形时,面积最大是1,所以滑动过程中,四边形OACB的面积的最大值是1+
;故结论③正确;
(另一种是二次函数,设OA=x,则OB=
,S△AOB=
x
=
=
≤1(等号仅当x=
时取得),所四边形OACB最大面积是1+
,故③正确)
 取AB的中点D,如图4,由于OD的长度始终是AB的一半,为1,且D为动点,O为定点,动点D到定点O的距离等于定长1的点轨迹是一个圆(弧),故④错,(如图5红色是AB的中点的轨迹,说明:除中点D和端点A、B外,其它点的轨迹是椭圆,那是高中的知识,设P(x,y)是AB上的一点,∠DAC=θ,且AP=a,则
取AB的中点D,如图4,由于OD的长度始终是AB的一半,为1,且D为动点,O为定点,动点D到定点O的距离等于定长1的点轨迹是一个圆(弧),故④错,(如图5红色是AB的中点的轨迹,说明:除中点D和端点A、B外,其它点的轨迹是椭圆,那是高中的知识,设P(x,y)是AB上的一点,∠DAC=θ,且AP=a,则
,解得:
+
=1(0<a<2,0<x<2,0<y<2),仅当a=1时即AB的中点轨迹是圆的一部分.)
取AB的中点D,(如图1)连OD、CD,则CO≤OC+OD(当O、D、C三点共线时取等号),此时OC=AB=2,知②正确;
(另外也可以这样考虑,如图2,∠AOB=∠ACB=90°,则∠AOB+∠ACB=180°,O、A、C、B四点共圆,OC为⊙D的弦,OC≤AB=2,当OC为⊙D的
 直径时,OC最大是2,也得结论②正确;
直径时,OC最大是2,也得结论②正确;由于△ABC的面积是
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
(另一种是二次函数,设OA=x,则OB=
| 4-x2 |
| 1 |
| 2 |
| 4-x2 |
| 1 |
| 2 |
| x2(4-x2) |
| 1 |
| 2 |
| -(x2-2)2+4 |
| 2 |
| ||
| 2 |
 取AB的中点D,如图4,由于OD的长度始终是AB的一半,为1,且D为动点,O为定点,动点D到定点O的距离等于定长1的点轨迹是一个圆(弧),故④错,(如图5红色是AB的中点的轨迹,说明:除中点D和端点A、B外,其它点的轨迹是椭圆,那是高中的知识,设P(x,y)是AB上的一点,∠DAC=θ,且AP=a,则
取AB的中点D,如图4,由于OD的长度始终是AB的一半,为1,且D为动点,O为定点,动点D到定点O的距离等于定长1的点轨迹是一个圆(弧),故④错,(如图5红色是AB的中点的轨迹,说明:除中点D和端点A、B外,其它点的轨迹是椭圆,那是高中的知识,设P(x,y)是AB上的一点,∠DAC=θ,且AP=a,则
|
| x2 |
| (2-a)2 |
| y2 |
| a2 |
点评:本题考查了解直角三角形的运用、四点共圆的性质、三角形的内角和定理、三角形的面积公式以及二次函数的性质题目综合性很强,对学生的解题能力要求很高,是一道不错的中考题目.

练习册系列答案
相关题目
 如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )| A、5对 | B、4对 | C、3对 | D、2对 |
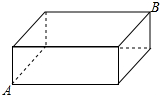 如图,是一个长9m,宽7m,高5m的仓库,在其内壁的A处有一只壁虎,B处有一只蚊子,则壁虎爬到蚊子处的最短距离为( )m.
如图,是一个长9m,宽7m,高5m的仓库,在其内壁的A处有一只壁虎,B处有一只蚊子,则壁虎爬到蚊子处的最短距离为( )m.| A、21m | B、15m |
| C、12m | D、13m |
有下列函数:①y=x-2;②y=-
;③y=-x2+(x+1)(x-2);④y=-
,其中是一次函数的有( )个.
| 2 |
| x |
| x |
| 2 |
| A、1个 | B、2个 | C、3个 | D、0个 |
下列说法中,正确的是( )
| A、两个互补的角中必有一个是钝角 |
| B、一个角的补角一定比这个角大 |
| C、互补的两个角中,至少有一个角大于或等于直角 |
| D、相等的角是对顶角 |
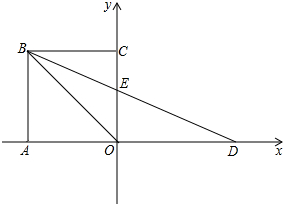 如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在x轴的正半轴上,且OD=OB,BD交OC于点E.
如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在x轴的正半轴上,且OD=OB,BD交OC于点E.