题目内容
边长为4的正方形的中心角是 ,边心距是 ,半径是 .
考点:正多边形和圆
专题:
分析:运用正方形的性质,以及与外接圆的关系,可分别求出中心角,边心距以及其半径.
解答: 解:∵正方形的边长为4,
解:∵正方形的边长为4,
由中心角只有四个可得出
=90°,
∴中心角是90°,
正方形的外接圆半径是:sin∠AOC=
,
∵AC=
=2,∠AOC=45°,
∴OA=
×4=2
,
tan∠AOC=
,
∵AC=
=2,∠AOC=45°,
∴边心距为:2.
故答案为:90°,2,2
.
 解:∵正方形的边长为4,
解:∵正方形的边长为4,由中心角只有四个可得出
| 360° |
| 4 |
∴中心角是90°,
正方形的外接圆半径是:sin∠AOC=
| AC |
| OA |
∵AC=
| 4 |
| 2 |
∴OA=
| ||
| 2 |
| 2 |
tan∠AOC=
| AC |
| OC |
∵AC=
| 4 |
| 2 |
∴边心距为:2.
故答案为:90°,2,2
| 2 |
点评:此题主要考查了正方形的性质与正方形与它的外接圆的关系,题目比较典型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列结论中,正确的有( )
①在数轴上,右边的点总大于左边的点;
②一个数的绝对值越大,表示它的点在数轴上离原点越远;
③两个负数,绝对值大的数反而小;
④正数和分数统称有理数;
⑤正有理数和负有理数统称为有理数.
①在数轴上,右边的点总大于左边的点;
②一个数的绝对值越大,表示它的点在数轴上离原点越远;
③两个负数,绝对值大的数反而小;
④正数和分数统称有理数;
⑤正有理数和负有理数统称为有理数.
| A、2个 | B、3个 | C、4个 | D、5个 |
在平面直角坐标器中,某个图形经过了一定的变化,大小和形状没有改变,那么这个图形上的各点的坐标有可能作了如下那一项改变?( )
| A、横纵坐标分别成2 | ||
B、横纵坐标分别变成原来的
| ||
| C、横坐标保持不变,纵坐标分别加2 | ||
| D、纵坐标保持不变,横坐标变为原来的2倍 |
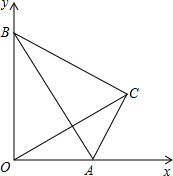 如图,在直角坐标系中,一个Rt△ABC的斜边AB在两坐标轴上滑动,AB=2,∠ABC=30°,下面说法正确的个数是( )个.
如图,在直角坐标系中,一个Rt△ABC的斜边AB在两坐标轴上滑动,AB=2,∠ABC=30°,下面说法正确的个数是( )个.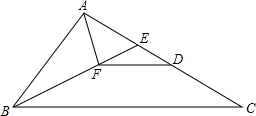 已知如图,点E在△ABC的边AC上,且∠AEB=∠ABC.
已知如图,点E在△ABC的边AC上,且∠AEB=∠ABC.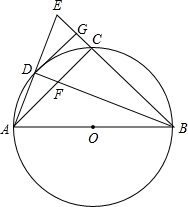 如图,AB是⊙O的直径,点C为弧AB的中点,∠ABC的角平分线交⊙O于点D,交AC于点F,AD、BC的延长线交于点E,DG⊥BE于点G.
如图,AB是⊙O的直径,点C为弧AB的中点,∠ABC的角平分线交⊙O于点D,交AC于点F,AD、BC的延长线交于点E,DG⊥BE于点G.