题目内容
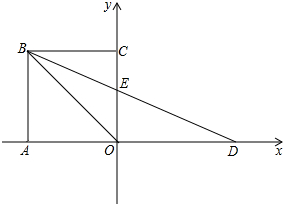 如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在x轴的正半轴上,且OD=OB,BD交OC于点E.
如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在x轴的正半轴上,且OD=OB,BD交OC于点E.(1)求∠BEC的度数.
(2)求过B、O、D三点的抛物线的解析式.
(3)求点E的坐标.
考点:正方形的性质,待定系数法求二次函数解析式
专题:
分析:(1)根据正方形的对角线平分一组对角可得∠AOB=∠COB=45°,根据等边对等角可得∠OBE=∠ODE,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OBE,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BEC=∠OBE+∠COB;
(2)根据正方形的边长写出点B的坐标,利用勾股定理求出OB,再写出点D的坐标,然后利用待定系数法求二次函数解析式解答;
(3)求出△BCE和△DOE相似,根据相似三角形对应边成比例列式求出
,然后求出OE的长度,再写出点E的坐标即可.
(2)根据正方形的边长写出点B的坐标,利用勾股定理求出OB,再写出点D的坐标,然后利用待定系数法求二次函数解析式解答;
(3)求出△BCE和△DOE相似,根据相似三角形对应边成比例列式求出
| CE |
| OE |
解答:解:(1)∵四边形AOCB是正方形,
∴∠AOB=∠COB=45°,
∵OD=OB,
∴∠OBE=∠ODE,
由三角形的外角性质得,∠OBE+∠ODE=∠AOB=45°,
∴∠OBE=
×45°=22.5°,
∴∠BEC=∠OBE+∠COB=22.5°+45°=67.5°;
(2)∵正方形AOCB的边长为1,
∴点B的坐标为(-1,1),OB=
=
,
∴点D的坐标为(
,0),
设过B、O、D三点的抛物线的解析式为y=ax2+bx(a≠0),
则
,
解得
.
所以抛物线解析式为y=(
-1)x2+(
-2)x;
(3)∵BC∥AD,
∴△BCE∽△DOE,
∴
=
=
,
∴OE=1×
=2-
,
所以点E的坐标为(0,2-
).
∴∠AOB=∠COB=45°,
∵OD=OB,
∴∠OBE=∠ODE,
由三角形的外角性质得,∠OBE+∠ODE=∠AOB=45°,
∴∠OBE=
| 1 |
| 2 |
∴∠BEC=∠OBE+∠COB=22.5°+45°=67.5°;
(2)∵正方形AOCB的边长为1,
∴点B的坐标为(-1,1),OB=
| 12+12 |
| 2 |
∴点D的坐标为(
| 2 |
设过B、O、D三点的抛物线的解析式为y=ax2+bx(a≠0),
则
|
解得
|
所以抛物线解析式为y=(
| 2 |
| 2 |
(3)∵BC∥AD,
∴△BCE∽△DOE,
∴
| CE |
| OE |
| BC |
| OD |
| 1 | ||
|
∴OE=1×
| ||
|
| 2 |
所以点E的坐标为(0,2-
| 2 |
点评:本题考查了正方形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等边对等角的性质,待定系数法求二次函数解析式,相似三角形的判定与性质,计算时要注意分母有理化.

练习册系列答案
相关题目
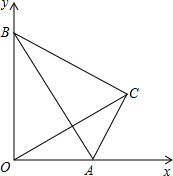 如图,在直角坐标系中,一个Rt△ABC的斜边AB在两坐标轴上滑动,AB=2,∠ABC=30°,下面说法正确的个数是( )个.
如图,在直角坐标系中,一个Rt△ABC的斜边AB在两坐标轴上滑动,AB=2,∠ABC=30°,下面说法正确的个数是( )个.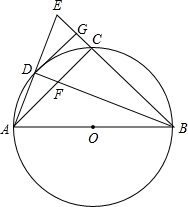 如图,AB是⊙O的直径,点C为弧AB的中点,∠ABC的角平分线交⊙O于点D,交AC于点F,AD、BC的延长线交于点E,DG⊥BE于点G.
如图,AB是⊙O的直径,点C为弧AB的中点,∠ABC的角平分线交⊙O于点D,交AC于点F,AD、BC的延长线交于点E,DG⊥BE于点G.
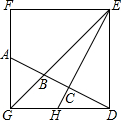 如图,DEFG为正方形,A、H分别是FG、GD的中点,DA分别与GE、HE相交于B、C,则AB:BC:CD=
如图,DEFG为正方形,A、H分别是FG、GD的中点,DA分别与GE、HE相交于B、C,则AB:BC:CD=