题目内容
多项式-2x2+4x-1的最大值是 ．
考点：二次函数的最值
专题：
分析：首先把多项式利用完全平方公式变为-2（x-1）2+1的形式，进一步利用非负数的性质解决问题．
解答：解：-2x2+4x-1=-2+1，
∵（x-1）2≥0，
∴-（x-1）2≤0，
∴-2x2+4x-1的最大值是1．
故答案为：1．
∵（x-1）2≥0，
∴-（x-1）2≤0，
∴-2x2+4x-1的最大值是1．
故答案为：1．
点评：此题考查完全平方公式的运用，以及非负数的性质，根据式子的特点，灵活运用公式解决问题．
练习册系列答案
相关题目
如图，在平面直角坐标系中，A（1，1），B（-1，1），C（-1，-2），D（1，-2）．把一条长为a个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按下列说法错误的是（ ）
| A、一个三角形中至少有一个角不少于60° |
| B、三角形的中线不可能在三角形的外部 |
| C、三角形的中线把三角形的面积平均分成相等的两部分 |
| D、直角三角形只有一条高 |
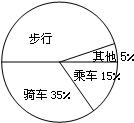某校对全校2560名学生的上学方式进行了一次抽样调查，右图是根据此次调查结果所绘制的一个未完成的扇形统计图，被调查的学生中骑车的有21人，则下列四种说法：下列说法中，不具有相反意义的一对量是（ ）
| A、向东2.5干米和向西2干米． |
| B、上升3米和下降1.5米 |
| C、零上6℃和零下5℃ |
| D、收入5000元和亏损5000元 |