题目内容
已知命题:等腰三角形底边上的中线和顶角的角平分线重合,证明这个命题,并写出它的逆命题,逆命题成立吗?
考点:命题与定理,等腰三角形的判定与性质
专题:
分析:根据证明的步骤,先写出已知、求证,再写出证明过程,最后写出逆命题即可.
解答:已知:△ABC中,AB=AC,AD是BC边的中线,
求证:∠BAD=∠CAD.
证明:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD.
它的逆命题是:底边上的中线和顶角的角平分线重合的三角形是等腰三角形,成立.
求证:∠BAD=∠CAD.

证明:在△ABD和△ACD中,
|
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD.
它的逆命题是:底边上的中线和顶角的角平分线重合的三角形是等腰三角形,成立.
点评:本题考查了命题与定理,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题,正确的命题叫真命题,错误的命题叫做假命题,判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α,β是一元二次方程x2-3x+1=0的两根,则α2+β2的值是( )
| A、6 | B、7 | C、8 | D、9 |
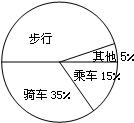 某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法:
某校对全校2560名学生的上学方式进行了一次抽样调查,右图是根据此次调查结果所绘制的一个未完成的扇形统计图,被调查的学生中骑车的有21人,则下列四种说法: