Question

20．已知直线l₁∥l₂，如图（1），等腰Rt△ABC的直角顶点A在l₁上，两个锐角顶点B、C都在直线l₂上，BC=2；等腰Rt△ABC沿直线l₂向右平移1个单位至Rt△A₁B₁C₁（点B₁与BC的中点重合）得图（2）；再将等腰Rt△A₁B₁C₁向右平移1个单位至Rt△A₂B₂C₂（点B₂与点C重合）得到图（3）；…；照此方式每次向右平移一个单位，则得到的图（8）中的三角形的个数共有（　　）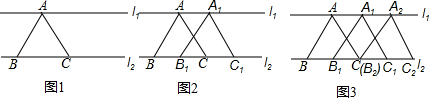

• A． 22
• B． 26
• C． 28
• D． 32

Answer 1

分析 观察图形可得图（2）中的三角形的个数为4，以后每个图形都比上一个图形的三角形多4，于是得到图（8）中的三角形的个数为4×7．

解答 解：图（2）中的三角形的个数为4=4×1=4，
图（3）中的三角形的个数为4+4=4×2=8，
图（4）中的三角形的个数为4+4+4=4×3=12，
所以图（8）中的三角形的个数为4×7=28．
故选C．

点评 本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．