题目内容
12.先化简,再求值:($\frac{a+2}{{a}^{2}-2a}$+$\frac{1-a}{{a}^{2}-4a+4}$)÷$\frac{a-4}{a}$,其中a满足a2-4a-1=0.分析 先根据分式混合运算的法则把原式进行化简,再根据a满足a2-4a-1=0得出(a-2)2=5,再代入原式进行计算即可.
解答 解:原式=$\frac{(a+2)(a-2)+a(1-a)}{a(a-2)^{2}}$•$\frac{a}{a-4}$
=$\frac{1}{{(a-2)}^{2}}$,
由a满足a2-4a-1=0得(a-2)2=5,
故原式=$\frac{1}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
2.在长春市“暖房子工程”实施过程中,某工程队做了面积为632000m2的外墙保暖.632000这个数用科学记数法表示为( )
| A. | 63.2×104 | B. | 6.32×105 | C. | 0.632×106 | D. | 0.632×106 |
3.下列图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.在下列的四个几何体中,其主视图与俯视图相同的是( )
| A. | 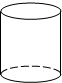 圆柱 | B. | 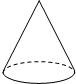 圆锥 | C. |  三棱柱 | D. | 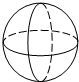 球 |
3.已知xa=3,xb=5,则xa-b=( )
| A. | -2 | B. | 15 | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
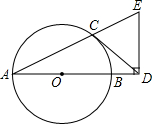 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.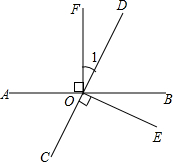 如图所示,已知∠1=40°,OE⊥CD,OF⊥AB,求∠BOE的度数.
如图所示,已知∠1=40°,OE⊥CD,OF⊥AB,求∠BOE的度数. 如图是一正方体的展开图,若正方体相对两个面上的式子的值相等,则32x-y=1.
如图是一正方体的展开图,若正方体相对两个面上的式子的值相等,则32x-y=1.