题目内容
17.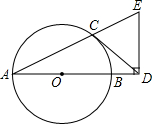 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.(1)求证:DC=DE;
(2)若tan∠CAB=$\frac{1}{2}$,AB=3,求BD的长.
分析 (1)利用切线的性质结合等腰三角形的性质得出∠DCE=∠E,进而得出答案;
(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,利用勾股定理得出BD的长.
解答 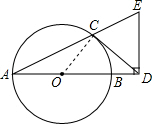 (1)证明:连接OC,
(1)证明:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE,
(2)解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,
在Rt△EAD中,
∵tan∠CAB=$\frac{1}{2}$,∴ED=$\frac{1}{2}$AD=$\frac{1}{2}$(3+x),
由(1)知,DC=$\frac{1}{2}$(3+x),在Rt△OCD中,
OC2+CD2=DO2,
则1.52+[$\frac{1}{2}$(3+x)]2=(1.5+x)2,
解得:x1=-3(舍去),x2=1,
故BD=1.
点评 此题主要考查了切线的性质以及以及勾股定理和等腰三角形的性质等知识,熟练应用切线的性质得出∠OCD=90°是解题关键.

练习册系列答案
相关题目
7. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
5.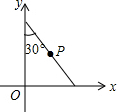 如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
 如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )| A. | ($\sqrt{3}$,1) | B. | (1,-$\sqrt{3}$) | C. | (2$\sqrt{3}$,-2) | D. | (2,-2$\sqrt{3}$) |
8.在如图的△ABC中,正确画出AC边上的高的图形是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,一个含有30°角的直角三角形的两个顶点放在一个长方形的对边上,若∠1=25°,则∠2=115°.
如图,一个含有30°角的直角三角形的两个顶点放在一个长方形的对边上,若∠1=25°,则∠2=115°.