题目内容
7.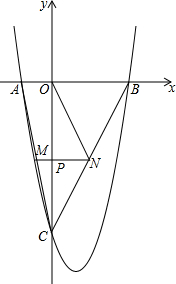 如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:
如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:(1)求抛物线的解析式;
(2)点P在线段OC上,过点P与x轴平行的直线交AC于点M,交BC于点N,且MN=4,求线段ON的长.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据相似三角形的判定与性质,可得CN与CB的关系,根据勾股定理,可得CB的长,根据直角三角形的性质,可得答案.
解答 解:(1)∵抛物线y=x2+bx+c经过点A(-2,0),点B(6,0),
∴$\left\{\begin{array}{l}{4-2b+c=0}\\{36+6b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=-12}\end{array}\right.$.
∴抛物线的解析式为y=x2-4x-12;
(2)∵OA=2,OB=6,
∴AB=OA+OB=8.
∵MN∥AB,MN=4,
∴△CMN∽△CAB,
∴$\frac{MN}{AB}$=$\frac{CN}{CB}$=$\frac{4}{8}$,
∴$\frac{CN}{CB}$=$\frac{1}{2}$,
∴点N为CB的中点,
∵点C坐标为(0,-12)
∴OC=12,
在Rt△COB中,根据勾股定理得:
CB=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{6}^{2}+1{2}^{2}}$=6$\sqrt{5}$,
∴ON=$\frac{1}{2}$BC=3$\sqrt{5}$.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,利用相似三角形的判定与性质得出N为BC的中点是解题关键,又利用了勾股定理,直角三角形的性质.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
19.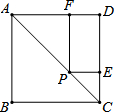 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )| A. | 3$\sqrt{2}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 6 |
16.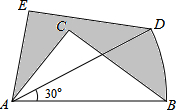 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )
如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )
 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )
如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )| A. | $\frac{25}{12}$π | B. | $\frac{4}{3}$π | C. | $\frac{3}{4}$π | D. | $\frac{5}{12}$π |
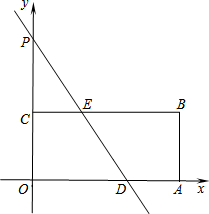 如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=kx+12与y轴交于点P,与边OA交于点D,与边BC交于点E.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=kx+12与y轴交于点P,与边OA交于点D,与边BC交于点E.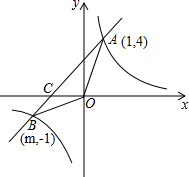 已知,如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
已知,如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),