题目内容
9. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先根据正方形的性质和旋转的性质得到∠AOF的度数,OA=OF,再根据等腰三角形的性质即可求得∠OFA的度数.
解答 解:∵正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,
∴∠AOF=90°+40°=130°,OA=OF,
∴∠OFA=(180°-130°)÷2=25°.
故选:C.
点评 考查了旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.同时考查了正方形的性质和等腰三角形的性质.

练习册系列答案
相关题目
19.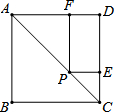 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )| A. | 3$\sqrt{2}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 6 |
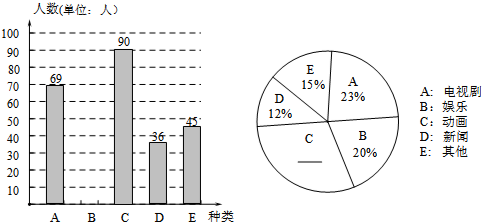
1.某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
(1)由题意知商品的最低销售单价是50元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
| x(件) | … | 5 | 10 | 15 | 20 | … |
| y(元/件) | … | 75 | 70 | 65 | 60 | … |
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
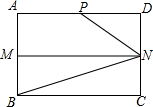 如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.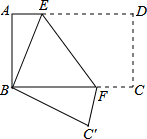 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )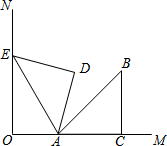 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.