题目内容
在锐角△ABC中,三条高交于点H,若∠BHC=110°,则∠BAC= °.
考点:三角形内角和定理
专题:
分析:先画出图形,根据CF⊥AB,BE⊥AC得出∠AFC=∠AEB=90°,再根据对顶角的性质得出∠EHF的度数,根据四边形内角和定理即可得出结论.
解答: 解:如图所示,
解:如图所示,
∵CF⊥AB,BE⊥AC,
∴∠AFC=∠AEB=90°,
∵∠EHF=∠BHC=110°,
∴∠A=360°-∠AFC-∠AEB-∠EHF=360°-90°-90°-110°=70°.
故答案为:70.
 解:如图所示,
解:如图所示,∵CF⊥AB,BE⊥AC,
∴∠AFC=∠AEB=90°,
∵∠EHF=∠BHC=110°,
∴∠A=360°-∠AFC-∠AEB-∠EHF=360°-90°-90°-110°=70°.
故答案为:70.
点评:本题考查的是三角形内角和定理,熟知三角形的三条高线相交于一点是解答此题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
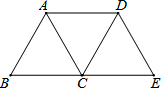 如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE.
其中正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
 如图,将周长为6的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为6的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )| A、6 | B、7 | C、8 | D、9 |
 如图,是反比例函数
如图,是反比例函数 如图是用一张长方形纸条折成的.如果∠1=130°,那么∠2=
如图是用一张长方形纸条折成的.如果∠1=130°,那么∠2= 如图,⊙O是△ABC的外接圆,已知∠ABO=30°,则∠ACB的为
如图,⊙O是△ABC的外接圆,已知∠ABO=30°,则∠ACB的为 江苏卫视《一站到底》栏目中,有一期的题目如图,两个天平都保持平衡,则三个球体的重量等于( )个正方体的重量.
江苏卫视《一站到底》栏目中,有一期的题目如图,两个天平都保持平衡,则三个球体的重量等于( )个正方体的重量.