题目内容
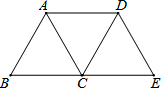 如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE.
其中正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:平移的性质,等边三角形的性质,菱形的判定
专题:
分析:根据等边三角形的性质得AB=BC,再根据平移的性质得AB=DC,AB∥DC,则可判断四边形ABCD为菱形,根据菱形的性质得AD=BC,BD、AC互相平分;同理可得四边形ACED为菱形;由于BD⊥AC,AC∥DE,易得BD⊥DE.
解答:解:∵△ABC为等边三角形,
∴AB=BC,
∵等边△ABC沿射线BC向右平移到△DCE的位置,
∴AB=DC,AB∥DC,
∴四边形ABCD为平行四边形,
而AB=BC,
∴四边形ABCD为菱形,
∴AD=BC,BD、AC互相平分,所以①②正确;
同理可得四边形ACED为菱形,所以③正确;
∵BD⊥AC,AC∥DE,
∴BD⊥DE,所以④正确.
故选D.
∴AB=BC,
∵等边△ABC沿射线BC向右平移到△DCE的位置,
∴AB=DC,AB∥DC,
∴四边形ABCD为平行四边形,
而AB=BC,
∴四边形ABCD为菱形,
∴AD=BC,BD、AC互相平分,所以①②正确;
同理可得四边形ACED为菱形,所以③正确;
∵BD⊥AC,AC∥DE,
∴BD⊥DE,所以④正确.
故选D.
点评:本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了等边三角形的性质和菱形的判定与性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若|a-2013|+(b+1)2012=0,则b4的值为( )
| A、-1 | B、1 |
| C、-2013 | D、2013 |
如图图形是按一定的规律排列的,依照此规律,第10个图形有( )条线段.


| A、125 | B、140 |
| C、155 | D、160 |
 如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为( )cm.
如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为( )cm.| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
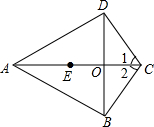 如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.