题目内容
12.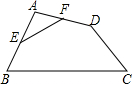 如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 连接BD,根据三角形中位线定理求出EF,根据勾股定理的逆定理得到∠BDC=90°,根据正切的定义计算即可.
解答 解: 连接BD,
连接BD,
∵E、F分别是AB、AD中点,
∴BD=2EF=4,
∵BD2+CD2=25,BC2=25,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴tanC=$\frac{BD}{CD}$=$\frac{4}{3}$,
故选:A.
点评 本题考查的是三角形中位线定理、勾股定理的逆定理、解直角三角形的知识,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
3.下列事件中,属于随机事件的有( )
①太阳东升西落
②投一枚骰子得到的点数是奇数
③买一张彩票中一等奖
④从日历本上任选一天为星期天.
①太阳东升西落
②投一枚骰子得到的点数是奇数
③买一张彩票中一等奖
④从日历本上任选一天为星期天.
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
1.下列命题中假命题是( )
| A. | 三角形的外角中至少有两个是钝角 | |
| B. | 直角三角形的两锐角互余 | |
| C. | 全等三角形的对应边相等 | |
| D. | 三角形三条边的垂直平分线一定交于三角形内一点 |
2.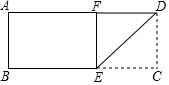 如图一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为F,若BE=6cm,则DE=( )
如图一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为F,若BE=6cm,则DE=( )
 如图一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为F,若BE=6cm,则DE=( )
如图一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为F,若BE=6cm,则DE=( )| A. | $4\sqrt{2}$cm | B. | 6cm | C. | 8cm | D. | 10cm |
 如图,在△ABC中,AB=AC,点D是底边上异于BC中点的一个点,∠1=∠2,DE=AC.运用以上条件(不再添加其它线),可以得到下面哪些结论:
如图,在△ABC中,AB=AC,点D是底边上异于BC中点的一个点,∠1=∠2,DE=AC.运用以上条件(不再添加其它线),可以得到下面哪些结论: