题目内容
2.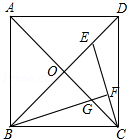 如图,正方形ABCD的对角线交于点O,点E是线段0D上一点,连接EC,作BF⊥CE于点F,交0C于点G.若AB=4,BF是∠DBC的角平分线,则OE的长为4-2$\sqrt{2}$.
如图,正方形ABCD的对角线交于点O,点E是线段0D上一点,连接EC,作BF⊥CE于点F,交0C于点G.若AB=4,BF是∠DBC的角平分线,则OE的长为4-2$\sqrt{2}$.
分析 利用BF是∠DBC的角平分线求得∠EBF=∠CBF,结合BF=BF,∠BFE=∠BFC=90°,可证明△BEF≌△BCF(ASA),所以BE=BC=4,根据Rt△BOC中对应的比例关系和三角函数可求得BO=2$\sqrt{2}$,所以OE=BE-BO=4-2$\sqrt{2}$.根据△BOG≌△COE可知OG=OE=4-2$\sqrt{2}$.
解答 解:∵BF是∠DBC的角平分线,
∴∠EBF=∠CBF,
∵BF⊥CE,
∴∠BFE=∠BFC=90°,
在△BEF和△BCF中,
$\left\{\begin{array}{l}{∠EBF=∠CBF}\\{BF=BF}\\{∠BFE=∠BFC}\end{array}\right.$,
∴△BEF≌△BCF(ASA),
∴BE=BC=4,
∵在Rt△BOC中,cos∠OBC=$\frac{BO}{BC}$,
即cos45°=$\frac{BO}{BC}$,
∴BO=BC•cos45°=2$\sqrt{2}$,
∴OE=BE-BO=4-2$\sqrt{2}$,
故答案为:4-2$\sqrt{2}$.
点评 主要考查了正方形的性质和全等三角形的判定.要掌握正方形中一些特殊的性质:四边相等,四角相等,对角线相等且互相平分.可利用这些等量关系求得三角形全等是解题的关键.

练习册系列答案
相关题目

 是二次函数
是二次函数 的图象上两点,则
的图象上两点,则 ____
____ (填“>”、“<”或“=” )
(填“>”、“<”或“=” )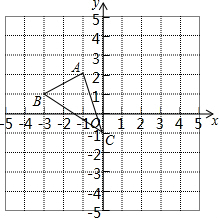 如图,图形中每一小格正方形的边长为1,已知△ABC
如图,图形中每一小格正方形的边长为1,已知△ABC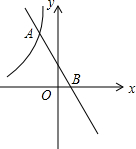 如图,一次函数y2=-2x+b(b为常数)的图象与反比例函数y1=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(-1,4).当y1<y2时,求x的取值范围.
如图,一次函数y2=-2x+b(b为常数)的图象与反比例函数y1=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(-1,4).当y1<y2时,求x的取值范围.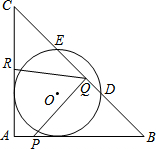 如图,在△ABC中,∠A=90°,AB=AC=12cm,半径为4cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1cm/s、xcm/s、1.5cm/s,运动时间为ts.
如图,在△ABC中,∠A=90°,AB=AC=12cm,半径为4cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1cm/s、xcm/s、1.5cm/s,运动时间为ts.