题目内容
11.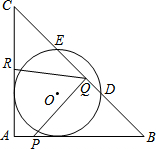 如图,在△ABC中,∠A=90°,AB=AC=12cm,半径为4cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1cm/s、xcm/s、1.5cm/s,运动时间为ts.
如图,在△ABC中,∠A=90°,AB=AC=12cm,半径为4cm的⊙O与AB、AC两边都相切,与BC交于点D、E.点P从点A出发,沿着边AB向终点B运动,点Q从点B出发,沿着边BC向终点C运动,点R从点C出发,沿着边CA向终点A运动.已知点P、Q、R同时出发,运动速度分别是1cm/s、xcm/s、1.5cm/s,运动时间为ts.(1)求证:BD=CE;
(2)若x=3,当△PBQ∽△QCR时,求t的值;
(3)设△PBQ关于直线PQ对称的图形是△PB'Q,求当t和x分别为何值时,点B′与圆心O恰好重合.
分析 (1)作辅助线连接AO并延长交BC于点H.连接OE、OD.由等腰三角形三线合一得出OH平分ED.再由CE=CH-EH,BD=BH-DH,即可得出BD=CE.
(2)在Rt△ABC中,易得出BC的值,利用△PBQ∽△QCR,得出$\frac{BP}{CQ}$=$\frac{BQ}{CR}$,列出关于t的式子,即可求出t的值.
(3)设⊙O与AB相切于点M,作辅助线连接AO并延长交BC于点H.连接OM、OB、OP、OQ,由点O与点B关于PQ对称,PQ垂直平分BO.可得OP=BP,OQ=BQ.又⊙O与AB相切于点M,可得出OM⊥AB.设BP=a,在Rt△OMP中,利用勾股定理即可得出a=5;由(1)可得AH是△ABC的高,BH,OH的值,设BQ=b,在Rt△OHB中,利用勾股定理即可得出b的值,即可得出t的值;由x=BQ÷3求解即可.
解答 证明:(1)如图1,连接AO并延长交BC于点H.连接OE、OD.
∵⊙O与AB、AC两边都相切,
∴点O到AB、AC两边的距离相等.
∴AH是∠CAB的平分线.
∵AB=AC,
∴AH⊥BC,AH平分BC.
∵OE=OD,OH⊥ED,
∴OH平分ED.
∵CE=CH-EH,BD=BH-DH,
且CH=BH,EH=DH,
∴BD=CE.
(2)解:在Rt△ABC中,BC=$\sqrt{122+122}$=12$\sqrt{2}$.
∵△PBQ∽△QCR,
∴$\frac{BP}{CQ}$=$\frac{BQ}{CR}$,即$\frac{12-t}{12\sqrt{2}-3t}$=$\frac{3t}{1.5t}$.解得t=$\frac{24\sqrt{2}-12}{5}$.
(3)解:设⊙O与AB相切于点M,连接AO并延长交BC于点H.连接OM、OB、OP、OQ,
∵点O与点B关于PQ对称,
∴PQ垂直平分BO.
∴OP=BP,OQ=BQ.
∵⊙O与AB相切于点M,
∴OM⊥AB.
设BP=a,在Rt△OMP中,(12-4-a)2+42=a2,解得a=5;
∵由(1)可得AH是△ABC的高,
∴BH=$\frac{12}{\sqrt{2}}$=$6\sqrt{2}$,OH=2$\sqrt{2}$,
设BQ=b,在Rt△OHB中,(6$\sqrt{2}$-b)2+(2$\sqrt{2}$)2=b2,解得b=$\frac{10\sqrt{2}}{3}$.
t=$\frac{12-5}{1}$=7s;x=$\frac{10\sqrt{2}}{3}$÷7=$\frac{10\sqrt{2}}{21}$cm.
点评 本题主要考查了圆的综合题,涉及等腰三角形的性质,勾股定理,切线的性质等知识,解题的关键是正确作出辅助线,灵活运用对称的图形的性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案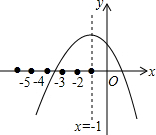 小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=-3.4,则方程的另一个近似根(精确到0.1)为( )
小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=-3.4,则方程的另一个近似根(精确到0.1)为( )| A. | 4.4 | B. | 3.4 | C. | 2.4 | D. | 1.4 |

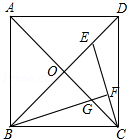 如图,正方形ABCD的对角线交于点O,点E是线段0D上一点,连接EC,作BF⊥CE于点F,交0C于点G.若AB=4,BF是∠DBC的角平分线,则OE的长为4-2$\sqrt{2}$.
如图,正方形ABCD的对角线交于点O,点E是线段0D上一点,连接EC,作BF⊥CE于点F,交0C于点G.若AB=4,BF是∠DBC的角平分线,则OE的长为4-2$\sqrt{2}$.
 如图,长方形ABCD恰好可分成7个形状大小相同的小长方形,如果小长方形的面积是3,则长方形ABCD的周长是( )
如图,长方形ABCD恰好可分成7个形状大小相同的小长方形,如果小长方形的面积是3,则长方形ABCD的周长是( )
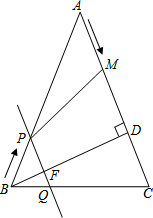 已知如图,在△ABC中,AB=AC=10$\sqrt{2}$cm,∠BAC=45°,BD⊥AC于D,点M从点A出发,沿AC方向匀速运动,速度为2cm/s,同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,交BD于F,连接PM,设运动时间为t(s)(0<t<5$\sqrt{2}$),解答下列问题:
已知如图,在△ABC中,AB=AC=10$\sqrt{2}$cm,∠BAC=45°,BD⊥AC于D,点M从点A出发,沿AC方向匀速运动,速度为2cm/s,同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,交BD于F,连接PM,设运动时间为t(s)(0<t<5$\sqrt{2}$),解答下列问题: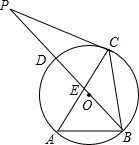 如图,在锐角△ABC中,∠A=60°,⊙O是△ABC的外接圆,射线BO交AC于E点.交⊙O于D点,P是射线BD上一点,且CP=CB.
如图,在锐角△ABC中,∠A=60°,⊙O是△ABC的外接圆,射线BO交AC于E点.交⊙O于D点,P是射线BD上一点,且CP=CB.