题目内容
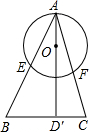 已知AD是⊙O的直径,AD′⊥BC,AB、AC分别与圆相交于E、F,那么下列等式中一定成立的是( )
已知AD是⊙O的直径,AD′⊥BC,AB、AC分别与圆相交于E、F,那么下列等式中一定成立的是( )| A、AE•BF=AF•CF |
| B、AE•AB=AO•AD′ |
| C、AE•AB=AF•AC |
| D、AE•AF=AO•AD |
考点:切割线定理
专题:
分析:连接DE、DF,如图,先根据圆周角定理由AD是⊙O的直径得到∠AED=∠AFD=90°,而∠AD′B=∠AD′C=90°,则可判断B、D′、D、E四点共圆,C、D′、D、F四点共圆,然后根据切割线定理得AE•AB=AD•AD′,AF•AC=AD•AD′,则AE•AB=AF•AC.
解答:解: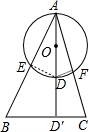 连接DE、DF,如图,
连接DE、DF,如图,
∵AD是⊙O的直径,
∴∠AED=∠AFD=90°,
∵AD′⊥BC,
∴∠AD′B=∠AD′C=90°,
∴B、D′、D、E四点共圆,C、D′、D、F四点共圆,
∴AE•AB=AD•AD′,AF•AC=AD•AD′,
∴AE•AB=AF•AC.
故选C.
 连接DE、DF,如图,
连接DE、DF,如图,∵AD是⊙O的直径,
∴∠AED=∠AFD=90°,
∵AD′⊥BC,
∴∠AD′B=∠AD′C=90°,
∴B、D′、D、E四点共圆,C、D′、D、F四点共圆,
∴AE•AB=AD•AD′,AF•AC=AD•AD′,
∴AE•AB=AF•AC.
故选C.
点评:本题考查了切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.也考查了圆周角定理和四点共圆的判定方法.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
若x2+xy+y2=m,x2-xy+y2=n,则x2+y2可用m,n表示为( )
| A、m+n | ||
| B、m-n | ||
C、
| ||
D、
|
一个数的相反数是非负数,这个数一定是( )
| A、正数或零 | B、非零的数 |
| C、负数或零 | D、零 |
 如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )
如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )| A、45 | B、50 | C、60 | D、90 |
在一次数学考试中,七年级(1)班20名男生平均得m分,26名女生平均得n分,则这个班全体同学的平均分是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
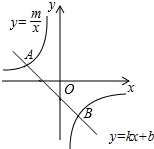 如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y=
如图,在直角坐标系中,一次函数y=kx+b的图形与反比例函数y= 如图所示,AC⊥BC,AD⊥BD,试证明:A、B、C、D在同一圆上.
如图所示,AC⊥BC,AD⊥BD,试证明:A、B、C、D在同一圆上.