题目内容
菱形ABCD的周长为20cm,DE⊥AB,垂足为E,
=
,则下列结论正确的个数有( )
①DE=3cm;②BE=1cm;③菱形的面积为15cm2;④BD=2
cm.
| DE |
| DA |
| 3 |
| 5 |
①DE=3cm;②BE=1cm;③菱形的面积为15cm2;④BD=2
| 10 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:菱形的性质
专题:
分析:利用菱形的性质结合勾股定理得出AE的长,进而判断各选项即可.
解答: 解:如图所示:∵菱形ABCD的周长为20cm,
解:如图所示:∵菱形ABCD的周长为20cm,
∴AD=CD=AB=BC=5cm,
∵DE⊥AB,垂足为E,
=
,
∴DE=3cm,故①正确;
∴AE=
=4(cm),
∴BE=1cm,故②正确;
则菱形的面积为:DE×AB=3×5=15(cm2),故③正确;
在Rt△BDE中,DB=
=
(cm),故④错误.
故正确的有3个.
故选:C.
 解:如图所示:∵菱形ABCD的周长为20cm,
解:如图所示:∵菱形ABCD的周长为20cm,∴AD=CD=AB=BC=5cm,
∵DE⊥AB,垂足为E,
| DE |
| DA |
| 3 |
| 5 |
∴DE=3cm,故①正确;
∴AE=
| AD2-DE2 |
∴BE=1cm,故②正确;
则菱形的面积为:DE×AB=3×5=15(cm2),故③正确;
在Rt△BDE中,DB=
| DE2+BE2 |
| 10 |
故正确的有3个.
故选:C.
点评:此题主要考查了菱形的性质以及勾股定理,得出DE的长是解题关键.

练习册系列答案
相关题目
下列各对数中,互为相反数的有( )
(-1)与+(-1),+(+1)与-1,-(-2)与+(-2),+[-(+1)]与-[+(-1)],-(+2)与-(-2),-(-
)与+(+
).
(-1)与+(-1),+(+1)与-1,-(-2)与+(-2),+[-(+1)]与-[+(-1)],-(+2)与-(-2),-(-
| 1 |
| 3 |
| 1 |
| 3 |
| A、6对 | B、5对 | C、4对 | D、3对 |
已知在Rt△ABC中,∠ACB=Rt∠,AC=5,BC=12,则Rt△ABC的外接圆的半径为( )
| A、12 | ||
B、
| ||
| C、6 | ||
D、
|
若x2+xy+y2=m,x2-xy+y2=n,则x2+y2可用m,n表示为( )
| A、m+n | ||
| B、m-n | ||
C、
| ||
D、
|
按照如下排列规律,第103个图形是( )
□△○△□△○△□△○△□….
□△○△□△○△□△○△□….
| A、□ | B、△ | C、○ | D、不能确定 |
 如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )
如图,△ABC是等边三角形,D是BC上一点,若将△ADC绕点A顺时针旋转n度后到达△AEB的位置,则n的值为( )| A、45 | B、50 | C、60 | D、90 |
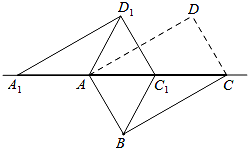 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1. 已知AC=6,∠ACB=30°,若要使四边形ABC1D1是菱形,则平移的距离等于
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1. 已知AC=6,∠ACB=30°,若要使四边形ABC1D1是菱形,则平移的距离等于