题目内容
17.已知|a-4|与(b-5)2互为相反数,c,d互为倒数,|e|=1,求$\frac{a-b}{e}$+2e+$\frac{3}{cd}$的值.分析 根据互为相反数两数之和为0,互为倒数两数之积为1,得到a、b与cd的值,绝对值是的数是±1.代入所求式子计算即可求出值.
解答 解:∵|a-4|与(b-5)2互为相反数,
∴|a-4|+(b-5)2=0,
∴a-4=0,b-5=0,
∴a=4,b=5,
∵c,d互为倒数,
∴cd=1,
∵|e|=1,
∴e=±1,
当e=1时,原式=$\frac{4-5}{1}$+2×1+$\frac{3}{1}$=-1+2+3=4.
当e=-1时,原式=$\frac{4-5}{-1}$+2×(-1)+3=1-2+3=2.
点评 此题考查了有理数的混合运算,相反数,绝对值以及倒数,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
 已知:线段a、b;
已知:线段a、b;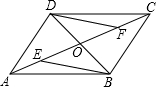 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF,求证:BE=DF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF,求证:BE=DF.