题目内容
8.阅读下列多项式因式分解的过程:x2-2x-8=x2-2•x•1+12-12-8=(x-1)2-9=(x-1)2-32=(x-1+3)(x-1-3)=(x+2)(x-4)
这种把多项式分解因式的方法叫做“配方法”,请你根据上面的材料解答下列问题:
(1)利用完全平方公式填空:x2+8x+(4)2=(x+4)2;
(2)用“配方法”把多项式x2-6x-16分解因式;
(3)如果关于x的二次三项式x2+10x+m在实数范围内不能因式分解,求实数m的取值范围.
分析 (1)利用完全平方公式的结构特征判断即可确定出结果;
(2)多项式配方后,利用完全平方公式及平方差公式分解即可;
(3)多项式配方后,利用完全平方公式化简,根据题意确定出m的范围即可.
解答 解:(1)x2+8x+42=(x+4)2;
故答案为:4;4;
(2)x2-6x-16=x2-2•3•x+32-32-16=(x-3)2-25=(x-3+5)(x-3-5)=(x+2)(x-8);
(3)x2+10x+m=(x+5)2-25+m=(x+5)2+(m-25),
当m-25>0,即m>25时,多项式x2+10x+m=(x+5)2+(m-25)在实数范围内不能因式分解,
则实数m的取值范围是m>25.
点评 此题考查了因式分解-十字相乘法,以及实数范围内分解因式,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),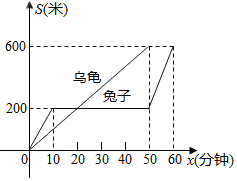 “龟兔赛跑”是同学们熟悉的寓言故事,图中表示路程S(米)与时间t(分)之间的关系,那么可以知道:
“龟兔赛跑”是同学们熟悉的寓言故事,图中表示路程S(米)与时间t(分)之间的关系,那么可以知道: