题目内容
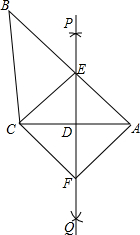 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图:①分别以A,C为圆心,大于
| 1 |
| 2 |
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)如果AE=5,求四边形AECF的周长.
考点:作图—基本作图,全等三角形的判定与性质
专题:
分析:(1)由作图知:PQ为线段AC的垂直平分线,从而得到AE=CE,AD=CD,然后根据CF∥AB得到∠EAC=∠FCA,∠CFD=∠AED,利用ASA证得两三角形全等即可;
(2)根据全等得到AE=CF,然后根据EF为线段AC的垂直平分线,得到EC=EA,FC=FA,从而得到EC=EA=FC=FA,利用四边相等的四边形是菱形判定四边形AECF为菱形,进而可求出其周长.
(2)根据全等得到AE=CF,然后根据EF为线段AC的垂直平分线,得到EC=EA,FC=FA,从而得到EC=EA=FC=FA,利用四边相等的四边形是菱形判定四边形AECF为菱形,进而可求出其周长.
解答:(1)证明:由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA);
(2)解:∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形,
∵AE=5,
∴四边形AECF的周长为20.
∴AE=CE,AD=CD,
∵CF∥AB
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
|
∴△AED≌△CFD(ASA);
(2)解:∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形,
∵AE=5,
∴四边形AECF的周长为20.
点评:本题考查了菱形的判定、全等的判定与性质及基本作图,解题的关键是了解通过作图能得到直线的垂直平分线.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
下列关于角平分线的说法正确的是( )
| A、若∠AOP=∠BOP,则射线OP是∠AOB的角平分线 | ||
| B、若∠AOP=2∠BOP,则射线OP是∠AOB的角平分线 | ||
C、若∠AOP=
| ||
| D、若2∠AOP=2∠BOP=∠AOB,则射线OP是∠AOB的角平分线 |
下列图形中轴对称图形的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
 如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为18cm2?
如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为18cm2?