题目内容
化简求值：
+
+
+…+
+
，其中a=2006．
| 1 |
| a(a+2) |
| 1 |
| (a+2)(a+4) |
| 1 |
| (a+4)(a+6) |
| 1 |
| (a+2002)(a+2004) |
| 1 |
| (a+2004)(a+2006) |
考点：分式的化简求值
专题：
分析：根据
=
（
-
），
=
（
-
），…，
=
（
-
），可得原式的值为
（
-
），再代入a=2006即可．
| 1 |
| a(a+2) |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a+2 |
| 1 |
| (a+2)(a+4) |
| 1 |
| 2 |
| 1 |
| a+2 |
| 1 |
| a+4 |
| 1 |
| (a+2004)(a+2006) |
| 1 |
| 2 |
| 1 |
| a+2004 |
| 1 |
| a+1006 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a+2006 |
解答：解：∵
=
（
-
），
=
（
-
），…，
=
（
-
），
∴原式=
（
-
+
-
+…+
-
），
（
-
），
∵a=2006，
∴原式=
（
-
）
=
×
=
．
| 1 |
| a(a+2) |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a+2 |
| 1 |
| (a+2)(a+4) |
| 1 |
| 2 |
| 1 |
| a+2 |
| 1 |
| a+4 |
| 1 |
| (a+2004)(a+2006) |
| 1 |
| 2 |
| 1 |
| a+2004 |
| 1 |
| a+1006 |
∴原式=
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a+2 |
| 1 |
| a+2 |
| 1 |
| a+4 |
| 1 |
| a+2004 |
| 1 |
| a+1006 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a+2006 |
∵a=2006，
∴原式=
| 1 |
| 2 |
| 1 |
| 2006 |
| 1 |
| 4012 |
=
| 1 |
| 2 |
| 1 |
| 4012 |
=
| 1 |
| 8024 |
点评：本题考查了分式的化简求值，把分式中的
化为
（
-
）是解题的关键．
| 1 |
| a(a+2) |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a+2 |
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如图，直线y=-x+1与x轴，y轴分别交于B，A两点，动点P在线段AB上移动，以P为顶点作∠OPQ=45°交x轴于点Q．
如图，已知DE∥BC，AD：BD=2：3，则
如图，某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长20m），另三边用木栏围成，木栏长48m．
由4个相同的小立方块搭成的几何体如图所示，它的俯视图是（ ）A、 |
B、 |
C、 |
D、 |
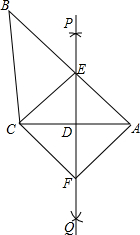如图，已知△ABC，按如下步骤作图：